In Python, range() is most commonly used in for loops to iterate over a known range of numbers. But that’s not all it can do! There are other interesting uses of range(). For example, you can pick out elements of a range or check whether a given number belongs to a range of numbers. The latter operation is known as a membership test.
Python’s range() objects support most of the operations that you’ve come to expect from lists. For example, you can calculate the total length, pick out a number at a given index, and iterate over each element in a range. Assume that you have a range of the first ten million integers and a list with the same numbers:
>>> numbers_as_range = range(10_000_000)
>>> numbers_as_list = list(numbers_as_range)
For many operations, you can treat these objects as interchangeable. Both ranges and lists support indexing items and calculating length:
>>> numbers_as_range[123]
123
>>> numbers_as_list[123]
123
>>> len(numbers_as_range)
10000000
>>> len(numbers_as_list)
10000000
Additionally, you can iterate over each object or check if a certain element is a member. For example, you can use the in operator to check whether -1 is part of any of these containers:
>>> -1 in numbers_as_range
False
>>> -1 in numbers_as_list
False
Because the range and the list only include non-negative numbers, -1 is not a member. However, the time Python takes to figure this out is vastly different for the two data structures:
>>> from timeit import timeit
>>> timeit("-1 in numbers_as_range", globals=globals(), number=100)
4.68301093652801e-06
>>> timeit("-1 in numbers_as_list", globals=globals(), number=100)
5.704572553362310
Here, you use timeit to measure the running time of the code. The reported numbers indicate how many seconds Python spent executing each command a hundred times.
Note the e-06 suffix in the first number. It’s scientific notation that means that the number in front of the suffix represents microseconds. If you compare the numbers, then you’ll see that searching for—and not finding—an element is several orders of magnitude slower in the list than in the range object.
In this tutorial, you’ll investigate how range() works under the hood and learn why Python’s range() membership tests are so fast. If you want to brush up on how to work with range(), then you should have a look at The Python range() Function first. You can click the link below to download some example code that you’ll be exploring in this tutorial:
Free Bonus: Click here to download the sample code that you’ll use to explore how Python runs such quick membership tests on range().
In Short: A Formula Determines Membership in a Python Range
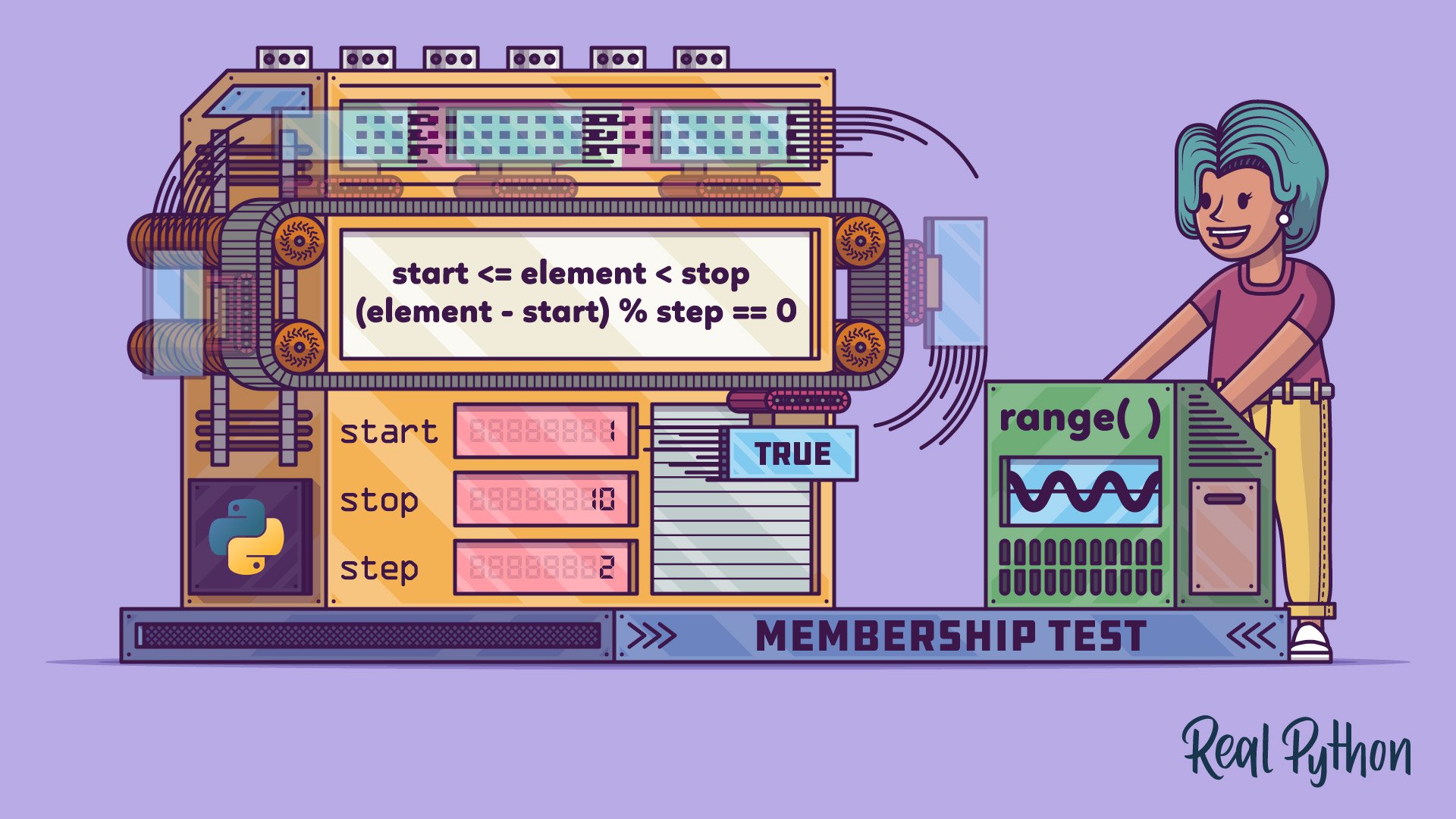
In Python, three numbers define a range: start, stop, and step. The range will begin at start and then contain every step integer that’s smaller than stop. For example, if start = 1, stop = 10, and step = 2, then the range will be the odd numbers less than ten. Namely, one, three, five, seven, and nine.
A list is much more flexible. It can contain any number of elements, and the elements can be of any type. It’s possible to have repeated elements. A list is often not sorted. In fact, it’s possible to have lists that Python can’t order, as the elements can be of mixed types that aren’t comparable.
All this flexibility has a price. To check if a list contains a particular element, Python needs to look through the list—one element at a time—until it finds a match. In principle, the operation looks something like this:
>>> def list_contains(element, list_elements):
... for list_element in list_elements:
... if list_element == element:
... return True
... return False
...
This function loops over all the list elements until it finds a match. If that match happens to be one of the first elements in the list, then it returns quickly. But if element isn’t in the list, then the function needs to inspect all the elements in the list to reach this conclusion.
If you’re working with ranges, then Python can take a shortcut and use a formula instead. With the following function, you can implement such a calculation:
>>> def range_contains(element, start, stop, step=1):
... return start <= element < stop and (element - start) % step == 0
...
You’ll look at the details of how range_contains() works soon. For now, you’ll use it to check if a range contains a given element. Consider the odd numbers less than ten that you played with earlier:
>>> range_contains(7, start=1, stop=10, step=2)
True
>>> range_contains(4, start=1, stop=10, step=2)
False
Your function calls confirm that the range of odd numbers contains 7 but not 4. Now look closer at the implementation of range_contains(). It checks two conditions:
start <= element < stop(element - start) % step == 0
The first check ensures that element is in the required half-open interval. It needs to be greater than or equal to start and smaller than stop because range() isn’t inclusive of the stop value. The second condition uses the modulo operator (%) to confirm that element is a multiple of step away from start.
Note: The given formula doesn’t support negative steps, but you can use negative steps to decrement with range():
>>> range_contains(7, start=9, stop=0, step=-2)
False
>>> 7 in range(9, 0, -2)
True
If step is negative, then start becomes the largest number in the range. That means the first condition should be start >= element > stop in this case. The second condition holds for negative step values because the modulo operator will still work as intended.
By using range_contains(), you can determine whether an element is part of a range. The complexity of the calculations doesn’t depend on the size of the range, so these membership tests are reasonably fast, independent of the size of the range.
If you want to look for an element in a corresponding list, then you may end up having to look at all the items in the list. As the list grows, this will take more and more time. This is why testing for membership in a range is faster, in general, than in a list.
You’ve seen how—in principle—range() implements membership tests. In the next section, you’ll learn more about the general implementation of range().
How Does Python Implement range()?
Since range() is a core part of Python, it’s implemented in C, which certainly helps with its speed. At first glance, range() may look like a function. But if you dig deeper, then you’ll discover that range is a class, and range() is its constructor.
In this section, you’ll code a custom Range class that works mostly the same as the built-in range but is slower because it’s not implemented in C. Through this exercise, you’ll learn more about range() as well as Python’s data model. The data model defines special methods, also called dunder methods, that you can implement in a class to support common Python operations and operators like len(), the addition operator (+), and iteration.
For convenience, you’ll use data classes to define two classes, Range and _RangeIterator. The first one will approximate the built-in range, while the second will facilitate iteration with Range. Add the following code to a file named range_tools.py:
# range_tools.py
from dataclasses import dataclass
@dataclass
class Range:
start: int
stop: int
step: int = 1
This gives you a skeleton that you’ll expand throughout this section. You can already instantiate a Range object:
>>> from range_tools import Range
>>> Range(start=0, stop=10_000_000)
Range(start=0, stop=10000000, step=1)
>>> Range(start=1, stop=10, step=2)
Range(start=1, stop=10, step=2)
The step parameter is optional, with a default value of 1. Unlike for the built-in range, start isn’t optional here, but you can use named keyword arguments.
The most common use of ranges is in iteration, so you’ll implement that next. The iterator protocol dictates that you need to implement two special methods: .__iter__() and .__next__(). To conveniently support iterating over a range several times, you’ll use a non-public class, _RangeIterator. Each _RangeIterator instance remembers the state of one iteration. Add this class to the same file:
# range_tools.py
from dataclasses import dataclass, field
# ...
@dataclass
class _RangeIterator:
start: int
stop: int
step: int
_state: int | None = field(default=None, init=False)
def __next__(self):
if self._state is None:
self._state = self.start
else:
self._state += self.step
if self._state >= self.stop:
raise StopIteration
return self._state
You name _RangeIterator with a leading underscore to indicate that it’s a helper class and not something that you should call directly. In addition to including .start, .stop, and .step, you add an internal attribute named ._state that will keep track of the iteration. You initialize the value of ._state to None to indicate that the iteration hasn’t started.
Note: The syntax int | None indicates that .state can be either an integer or None. You can only use the vertical bar (|) in Python 3.10 and later. Otherwise, you can use typing.Optional and write Optional[int].
The .__next__() special method is responsible for calculating the next element. If .state is None, then the iteration hasn’t started, so you set the next element to .start. Otherwise, you increase the current element by .step. If the element is greater than or equal to .stop then you end the iteration by raising StopIteration. Finally, you return the value of the next element.
To complete the implementation of your custom Range as an iterator, you add .__iter__() to it:
# range_tools.py
# ...
@dataclass
class Range:
start: int
stop: int
step: int = 1
def __iter__(self):
return _RangeIterator(self.start, self.stop, self.step)
# ...
The .__iter__() special method is in charge of initializing the iterator. In this case, you only need to instantiate a _RangeIterator with proper parameters. You can now iterate over your custom Range objects. Restart your REPL session to pick up your latest updates. Then try to convert Range to a list:
>>> from range_tools import Range
>>> list(Range(start=1, stop=10, step=2))
[1, 3, 5, 7, 9]
Your custom Range correctly lists the odd numbers below ten. Any object that supports iteration automatically supports membership tests as well:
>>> 7 in Range(start=1, stop=10, step=2)
True
>>> 4 in Range(start=1, stop=10, step=2)
False
Python implements these membership tests under the hood by iterating over the object until it finds an element or exhausts the iterator. This will be slow for large ranges:
>>> from timeit import timeit
>>> numbers = Range(0, 10_000_000)
>>> timeit("-1 in numbers", globals=globals(), number=100)
78.16305017451504
Feel free to use a smaller range in your own experiments so that you don’t have to wait too long for the operations to finish. If you get impatient, then you can interrupt the calculation by pressing Ctrl+C on your keyboard.
Again you look for -1, which isn’t part of the range comprising the first ten million integers. In this example, it takes more than a minute to run the membership test one hundred times. Note that this is even slower than searching through the list as you did earlier, mainly because that list was implemented in C.
You can optimize the membership test by telling Python to use the same formula that you studied in the previous section. You do so by implementing the .__contains__() special method:
# range_tools.py
# ...
@dataclass
class Range:
start: int
stop: int
step: int = 1
def __iter__(self):
return _RangeIterator(self.start, self.stop, self.step)
def __contains__(self, element):
return (
self.start <= element < self.stop
and (element - self.start) % self.step == 0
)
# ...
The implementation of .__contains__() is the same as the implementation of range_contains() from the previous section. You can restart your Python interpreter to check the improved performance:
>>> from range_tools import Range
>>> from timeit import timeit
>>> numbers = Range(0, 10_000_000)
>>> timeit("-1 in numbers", globals=globals(), number=100)
8.584989233942503e-06
The checks that took more than a minute earlier now run in a few microseconds! When you want custom containers where you can exploit some structure to find members of the container, you should implement .__contains__().
The built-in range() supports more operations than iteration and membership testing. You can access individual elements, find the index of an element, calculate the length of a range, and so on. You can extend your own Range to support the same operations. Even though you won’t do so in this tutorial, you can click below to see the implementation of a more full-featured Range class:
Free Bonus: Click here to download the sample code that you’ll use to explore how Python runs such quick membership tests on range().
Is a Range Better Than a List?
You’ve seen that it’s generally faster to check if a particular element is a member of a range than it is to check for membership in a corresponding list. You’ve also learned that ranges support many of the same methods as lists. So, does that mean that a range is better than a list?
As with most such questions, the answer is loud and clear: it depends! If the numbers you need to represent are so well structured that you can use range(), then you should normally do so. A range will likely be faster than a list. It’ll also be more memory efficient because a range is uniquely defined by three numbers, while a list needs pointers to all of its elements.
If your data are harder to represent as a range, then a list is typically the better choice. The flexibility of lists is hard to beat!
Is a Range Better Than a Set or Dictionary?
There are container data structures in Python that are better suited for membership testing than lists. For example, sets and dictionaries are optimized for looking up values. They’re on par with and even faster than ranges for looking up values:
>>> from timeit import timeit
>>> numbers_as_range = range(10_000_000)
>>> numbers_as_set = set(numbers_as_range)
>>> numbers_as_dict = dict.fromkeys(numbers_as_range)
>>> timeit("-1 in numbers_as_range", globals=globals(), number=100)
4.408007953310404e-06
>>> timeit("-1 in numbers_as_set", globals=globals(), number=100)
2.8829672373830812e-06
>>> timeit("-1 in numbers_as_dict", globals=globals(), number=100)
3.396009560672908e-06
Searching through ranges, sets, or dictionaries takes about the same time. Both sets and dictionaries are much more flexible than ranges in terms of which elements they can contain. Indeed, they bring many of the same advantages as lists. For example, a set can contain all the prime numbers less than thirty, which a range couldn’t possibly represent:
>>> primes = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29}
A set can contain any Python object, including integers. Sets differ from lists in a few key aspects. Sets are unordered and can’t contain duplicate values. This means that there are many use cases where lists are more suitable than sets.
For example, if you’re recording a student’s scores on several exams, then you want to use a list. If you used a set, then you wouldn’t be able to see how the student’s performance has progressed over time. And if the student scored the same on two exams, then you’d lose one of those scores.
The timing results above indicate that a set is as fast—maybe even faster—than a range when checking whether an element is a member. There’s one caveat to this: it usually takes much longer to construct a set.
As you’ve seen, creating a range only requires recording three numbers, so it’s a performant operation:
>>> timeit("range(10_000_000)", number=100)
3.327196463941211e-05
Creating the corresponding set requires iterating over all the elements in the range. Therefore, it’ll be much slower for large sets:
>>> timeit("set(numbers_as_range)", globals=globals(), number=100)
37.61038364198480
Creating the set of ten million integers takes a significant amount of time. This means that you shouldn’t convert a range—or a list—to a set if you only need to do one membership lookup. However, if you’re doing repeated lookups, then the time to convert to a set will play a smaller role, and you can start to consider working with a set.
Dictionaries have some properties in common with sets. In particular, the keys of a dictionary behave mostly like a set, and as you confirmed earlier, finding elements among dictionary keys is fast. Still, the creation of the dictionary will often be the bottleneck:
>>> timeit("dict.fromkeys(numbers_as_range)", globals=globals(), number=100)
53.68100337609845
Initializing the dictionary with ten million keys is even slower than creating the set. You should only use a dictionary when you have some meaningful values to map each key to. Otherwise, a set will always be a better choice.
Conclusion
You’ve looked closely at range(), in particular why Python is so fast at finding out whether a particular element is part of a range. Along the way, you noticed that ranges share several characteristics with lists, and you’ve implemented your own Range class to explore these further. You also compared ranges’ performance of membership testing to that of lists, sets, and dictionaries.
Python’s data model is based on classes that implement special methods, often called dunder methods, like .__contains__(), .__iter__(), and .__len__(). You implemented some of these yourself. However, you can look at more of them by downloading the code for your Range class below:
Free Bonus: Click here to download the sample code that you’ll use to explore how Python runs such quick membership tests on range().
If you create your own classes, especially container data structures, then you should consider implementing explicit membership tests. Feel free to share your approach with the community in the comments below.