Every classical computer reduces the world to 0s and 1s. That binary framework has carried us from calculators to supercomputers, but some problems demand checking through 2n possibilities, a task that outpaces even the best machines. Now, what if information could exist in many states at once? That what if turned into a new model called quantum computation. Keep reading to break with binaries and get an overview of quantum computing basics.
By the end of this tutorial, you’ll understand that:
- Qubits, or quantum bits, are the basic units of quantum computing.
- A qubit can be in a superposition of 0 and 1. This means its state is a precise combination of both until measurement forces it to become either 0 or 1.
- The Bloch sphere is a standard way to visualize what a single qubit is doing.
- Entanglement creates strong correlations between two or more qubits, so measuring one tells you something about the others that you can’t explain with classical reasoning alone.
- Interference adjusts probability amplitudes so that wrong outcomes cancel and useful outcomes reinforce.
- Quantum hardware comes in different architectures, each with its own strengths and limitations.
- With Python libraries like Qiskit, you can build and run quantum circuits directly from Python.
Before you jump in, it’d be a good idea to go through the basics of classical computing. For example, knowing how bits work, what logic gates like AND and NOT do, and how you can determine the runtime complexity of an algorithm using Big O notation will help you understand the differences and advantages of quantum computing.
Get Your Code: Click here to download the free sample code to build a quantum circuit with Qiskit.
Take the Quiz: Test your knowledge with our interactive “Quantum Computing Basics With Qiskit” quiz. You’ll receive a score upon completion to help you track your learning progress:
Interactive Quiz
Quantum Computing Basics With QiskitTest your understanding of quantum computing basics, including superposition, qubits, entanglement, and key programming concepts.
Introduction to Quantum Computing
Quantum computing is the use of fundamental ideas from quantum mechanics to perform computations on special devices called quantum computers. Quantum systems can process information in ways that classical computers can’t. For example, they can explore multiple possibilities at once. This capability is thanks to concepts like superposition, entanglement, and interference, which you’ll explore soon.
To see how quantum computing works, it helps to look at the main quantum concepts in the context of computing and consider how they differ from classical approaches. You’ll cover these essential concepts in this tutorial.
Before moving on, keep in mind that quantum mechanics and quantum computing are often counterintuitive because they occur only at very small scales and not in everyday life. Even Niels Bohr, one of the founders of quantum theory, once said:
If quantum mechanics hasn’t profoundly shocked you, you haven’t understood it yet. (Source)
— Niels Bohr
Until recently, quantum computing was seen almost entirely as a physics domain, which kept people in other fields from applying it to their own work. The good news is that you don’t need to fully grasp the physics to understand how quantum computers can solve some problems more efficiently than classical ones. You can focus on the concepts and their implementation, and only later dive into the math if you want a deeper understanding.
To start, you’ll look at the basic unit of quantum information—quantum bits, or qubits—and learn how they differ from classical bits.
Qubits, Superposition, and Measurement
Qubits, or quantum bits, are the fundamental units of quantum information. A classical bit can only be 0 or 1, but a qubit can exist in a linear combination of both states at once, a property called superposition. Physically, this usually means that the qubit is a two-level system, such as two energy levels of an atom, that can exist in a superposition of those levels.
Superposition allows qubits to represent multiple possibilities at the same time, allowing quantum computing programs to explore many solutions in parallel.
To understand superposition, think of flipping a coin. A classical coin lands as either heads or tails. A quantum coin, however, can exist in a state that’s a blend of both heads and tails simultaneously. This is what physicists mean when they say a qubit exists in a linear combination of 0 and 1.
The key difference is that while the coin is spinning in the air, you know it’ll eventually be one or zero, whereas a qubit in superposition has no definite value until it is measured.
A qubit remains in superposition until you look at it, or more formally, measure it. Measurement forces the qubit to collapse into one of its basis states, 0 or 1, just like your usual classical bits. The outcome is probabilistic: You can’t know in advance which result you’ll get, but you can calculate the chances based on the qubit’s state beforehand.
Note: Looking at a superposition state actually destroys the superposition and collapses the qubit into a 0 or 1, or in other words, destroys the “quantumness” of the state. This means you can’t visualize qubits like bits. Instead, you view qubits as a mathematical object. However, they can be built from various physical systems: the spin of an electron, the polarization of a photon, or the energy levels of an atom.
Visualizing qubits and superposition is tricky and needs some extra mathematical tools. Turns out, a coin that’s free to rotate in three dimensions is a good analogy for one way of visualizing the quantum state of a qubit, called the Bloch Sphere.
The Bloch sphere is a geometrical, 3D sphere that’s often used to visualize qubits and their superpositions. The states of the qubits, including superpositions, are represented as points on the surface of a sphere. The closer the point is to the north pole, the higher the chance of measuring 0, and vice versa for 1:

For example, the north pole represents the state 0, and the south pole represents 1. What’s interesting about this sphere is that you can visualize superposition states as well:

Here, the vector is on the surface of the sphere and represents a superposition of 0 and 1. In this particular case, the qubit is in an equal superposition of 0 and 1, meaning it has a 50 percent chance of collapsing to either state when measured.
This means that while a classical computer with n bits can represent only one of 2n possible states at any given time, a quantum computer with n qubits can represent a superposition over all 2n potential states simultaneously. This is what allows quantum computing to explore many possible solutions at once instead of checking them one by one.
Superposition is powerful on its own, but it leads to two other uniquely quantum properties that make quantum computing different: entanglement and interference.
Entanglement and Interference
Another uniquely quantum property is entanglement, which one of the greatest physicists of the twentieth century described as:
Spooky action at a distance. (Source)
— Albert Einstein
When two qubits are entangled, their states become linked so that measuring one immediately tells you something about the other, regardless of how far apart they are.
For example, imagine two entangled qubits, A and B. If you measure A and it collapses to 0, then B is no longer independent. It’ll collapse in a correlated way, depending on the entangled state they share. The two qubits behave like a single system, even when separated by large distances.
This means that if you entangle your qubits, measuring one can reveal correlated information about another that you haven’t directly measured!
But entanglement alone isn’t enough. In quantum computing, qubits don’t just hold probabilities like classical dice. Instead, they carry amplitudes, numbers that can add or cancel each other out. When qubits interact, these amplitudes interfere. If two paths line up, the chances of seeing that outcome grow. If they conflict, the chances shrink or vanish.
This means you can design how qubits interact so that the wrong answers cancel out, and the right answers stand out.
Shor’s algorithm was built on these two concepts. Shor’s algorithm finds the prime factors of large numbers, a problem that becomes exponentially harder as numbers grow larger. In fact, this difficulty is the math problem protecting most encrypted internet traffic. Classical algorithms solve this problem in exponential time. For instance, factoring a 2048-bit number, which has 617 digits, requires astronomical time with current classical methods.
Shor’s algorithm runs in polynomial time on a sufficiently large quantum computer. Here’s how it works. Say you’re factoring 15 using the number 7. If you compute powers of 7 and take remainders when dividing by 15, you get a repeating sequence: 7, 4, 13, 1, 7, 4, 13, 1, and so on. The pattern cycles every 4 steps, and finding this period gives you the factors.
-
Superposition stores every exponent from 1 to millions in the qubits at the same time. The quantum computer isn’t cycling through try 1, try 2, try 3…. It’s holding all those attempts together as part of the same quantum state. This lets you evaluate the entire function across its range in one operation.
-
Entanglement correlates the qubits so that when you measure one and see the value 13, the others collapse to reveal only the positions where 13 appears: steps 3, 7, 11, and 15. Steps 3, 7, 11, and 15 appear without your checking them individually, and their regular 4-step spacing becomes visible.
-
Interference makes the repeating pattern grow stronger while irregular results fade out. The period of 4 becomes a clear measurement you can read directly. Once you have the period, you use it in a calculation that splits 15 into 3 and 5.
So, the core concepts of quantum mechanics give you the capability to explore more than one state at the same time. Next, you’ll dive deeper into why these ideas matter and how they can lead to practical advantages over classical computing.
The Power of Quantum Computing
Quantum computing matters because it promises speed-ups for problems that overwhelm classical computers. Some algorithms are already proven to be exponentially faster. Shor’s algorithm is one example, but there are others too. Grover’s algorithm, for instance, can search an unstructured database in about √N steps, compared to N steps classically.
Plus, classical computing is running into limits. In 1965, Gordon Moore noted that transistor counts on chips doubled about every year. This was later revised to every eighteen to twenty-four months.
Engineers have extended Moore’s Law for decades by shrinking transistor sizes to the atomic scale. But both physics and economics are now catching up. New fabrication plants require enormous investments, often running into tens of billions of dollars, and pushing performance gains has become harder each generation:
Moore’s Law is coming to an end and classical computing is reaching its limits just as our demand is starting to surge. (Source)
— Richard Debney, Vice President of BP
This is why the integration of quantum with classical systems has become so important.
Note: Quantum computing isn’t meant to replace classical computing. Instead, it’s seen as a complementary technology that can be used with classical supercomputers to solve specific problems more efficiently. Classical systems will still be the right choice for most tasks, especially routine calculations and data processing.
Quantum computing works particularly well for complex simulations, especially in chemistry and materials science, where quantum systems can naturally model other quantum systems. This is useful for drug discovery, material science, and understanding fundamental physics.
Apart from inherently quantum systems, recent research shows that quantum approaches are useful in other applied fields.
A joint study by IBM and Vanguard addressed one of finance’s hardest problems: portfolio optimization, which is the process of selecting a mix of assets like stocks and bonds that balances returns with real-world constraints. Turns out, hybrid quantum-classical methods can reach solutions comparable to state-of-the-art classical approaches. This suggests that quantum computing could eventually play a practical role in asset management.
Another promising demonstrated advantage is Google’s Quantum Echoes. The Quantum Echoes algorithm successfully measured the molecular structure of a real-world molecule thirteen thousand times faster than the best-known classical algorithm. The algorithm used Google’s Willow chip, a superconducting qubit device, showing that the state of quantum hardware is advancing rapidly.
One of the current goals of quantum computing is to demonstrate quantum advantage, sometimes called quantum supremacy. This is the point where a quantum computer solves a problem that’s infeasible for any classical machine. This milestone hasn’t been reached yet for broadly useful problems. IBM describes the path to practical quantum advantage in three phases:
- Awareness: Transitioning from traditional analytics-driven approaches to exploratory quantum research
- Readiness: Preparing infrastructure and workflows to integrate quantum computing into existing systems
- Advantage: Reaching the stage where hybrid quantum-classical systems deliver solutions impossible with classical computers alone
Right now, quantum computing sits between the first and second phases. A good number of researchers and industry leaders believe that quantum computing will become a practical tool within the next decade, and it’s time to start preparing:
There is no doubt that quantum computing technology will be ready for business this decade. There will be multiple million-qubit quantum machines by 2030. The question is, are you ready? (Source)
— Christian Weedbrook, CEO of Xanadu Quantum Technologies
This is why quantum computing matters to those who have access to real quantum hardware. But chances are, you only have a classical computer. So what’s the point of learning Python quantum libraries, which is what you’ll do shortly?
The point is that you can run quantum circuits on simulators and, once you have a working prototype, connect the same code to real quantum machines through cloud platforms offered by companies like IBM. In this tutorial, you’ll only design a circuit, but if you want to go further, the links provided will show you how to run your code on simulators first and then on actual hardware.
Now you might be asking, why hasn’t the promise of quantum advantage been fully realized yet? To answer that, you’d need to understand the state of current quantum hardware.
Quantum Computers and Their Limitations
To put superposition, entanglement, and interference into practice, you need specialized hardware. These devices use qubits built from different physical systems. Here are some common types:
-
Superconducting circuits: These are tiny electrical loops cooled to near absolute zero, where they lose all electrical resistance. The current flowing clockwise, counterclockwise, or in both directions simultaneously creates the qubit. IBM, Google, and Rigetti use this approach.
-
Trapped ions: Individual atoms are held precisely in place by electromagnetic fields. Their internal energy levels serve as the qubits, and lasers are used to manipulate them into superposition and create entanglement. IonQ and Quantinuum focus on this method.
-
Photons: These particles of light encode qubits using properties like polarization. Beam splitters and other optical devices control their paths and create interference. Xanadu and PsiQuantum work on photonic quantum computers.
Each approach has trade-offs. Superconducting qubits are fast but fragile. Trapped ions are more stable but slower to operate. Photons can work at room temperature but are harder to control precisely. The field hasn’t settled on a single best design yet.
Now, back to the elephant in the room. Throughout this article, quantum advantage has been presented as a theoretical concept rather than a practical reality. This is because current quantum computers are still in the early stages, often referred to as noisy intermediate-scale quantum (NISQ) devices. These machines face several fundamental limitations:
-
Quantum states are extremely fragile. They lose their quantum properties when they interact with the environment, a process called decoherence. This happens quickly, sometimes in microseconds, making it hard to complete calculations before the qubits break down.
-
Scaling up is another major hurdle. Most quantum computers today have fewer than a thousand qubits. Adding more qubits doesn’t just mean more power. It means exponentially more complexity in controlling them and keeping them from interfering with each other in unwanted ways.
-
Quantum systems are also inherently noisy. Even without external interference, the probabilistic nature of quantum mechanics introduces errors. Small imperfections in control pulses, crosstalk between neighboring qubits, and calibration drift all add up, making reliable computation difficult.
So, decoherence, scaling, and noise explain why quantum advantage remains mostly theoretical. But still, you can experiment with quantum computing today using simulators and cloud-based quantum processors. To do that, you need to learn how to program quantum computers.
Quantum Coding Within Reach
Now that you understand the core ideas, you’re ready to write your own program for a quantum computer. You do this by building quantum circuits that manipulate qubits with quantum gates, the quantum analog of classical logic gates. Some quantum gates have classical counterparts, like the NOT gate, which flips a bit from 0 to 1 or vice versa. But others, specifically those that harness superposition and entanglement, have no classical equivalent.
When it comes to designing quantum circuits, you have several libraries to choose from. IBM’s Qiskit, Microsoft’s Q#, Google’s Cirq, and Xanadu’s PennyLane are popular options, with PennyLane leaning into quantum machine learning. There are also platforms like Classiq that help you design scalable, visual circuits targeting different hardware.
Your First Quantum Circuit
In this section, you’ll use Qiskit, which is widely adopted and well documented. How it works is that you’ll use the Qiskit library in Python to write some instructions. Then, Qiskit translates these instructions using a quantum assembly language called OpenQASM into commands that a quantum processor can understand.
You can install Qiskit on your local machine using a virtual environment, or you can use a cloud platform like qBraid that allows you to run notebooks with a ready-made quantum environment directly in your browser.
Note: Instead of using a script, you can work in JupyterLab or a Jupyter Notebook if you prefer. In these interactive environments, you don’t need to save the graphs to view them, so you can omit writing them to a file.
Here’s how to install Qiskit with optional visualization dependencies like Matplotlib using pip. Make sure your Python version is 3.10 or above to be compatible with the latest version of Qiskit at the time of publication:
(venv) $ python -m pip install "qiskit[visualization]"
You can confirm that you’ve installed it correctly by opening a REPL session and checking the Qiskit version:
>>> import qiskit
>>> qiskit.__version__
'2.2.3'
Make sure your Qiskit version is 2.0.0 or above.
Since working with real quantum computers requires account authentication and extra setup steps, and even using simulators requires following the Qiskit Patterns, you’ll only focus on how to design a circuit using quantum gates.
To get a feel for how quantum circuits work, you’ll build a circuit that implements one of the very first quantum computing concepts you learned about: superposition. To do that, you’ll use the Hadamard gate. The Hadamard gate doesn’t have a classical equivalent, and it’s specifically designed to put a qubit into an equal superposition of 0 and 1.
Note: In superconducting qubits, the Hadamard gate is performed by applying a carefully timed microwave pulse that rotates the qubit’s quantum state into a balanced combination of both energy levels.
To start, you need to import the necessary classes and create a quantum circuit with one quantum register to hold your qubit and another classical register to hold the results of the measurement. Here’s how you can do it:
quantum_circuit.py
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister
qr = QuantumRegister(1, name="quantum")
cr = ClassicalRegister(1, name="classical")
qc = QuantumCircuit(qr, cr)
qc.draw("mpl", filename="quantum_circuit.png")
You’re importing the ClassicalRegister class to store your classical bit for measurement results, the QuantumCircuit class from Qiskit to build your circuit, and the QuantumRegister class to store your qubit. Then, you create a quantum register with one qubit and a classical register with one bit, with corresponding names. After that, you create a quantum circuit that combines both registers.
To visualize the circuit, you can use the .draw() method with the "mpl" option to get a Matplotlib rendering.
Note: If you’re working in a notebook environment, then you can omit the filename argument. The graph will display in the output cell.
When you view the generated file, quantum_circuit.png, then you should see something like this:
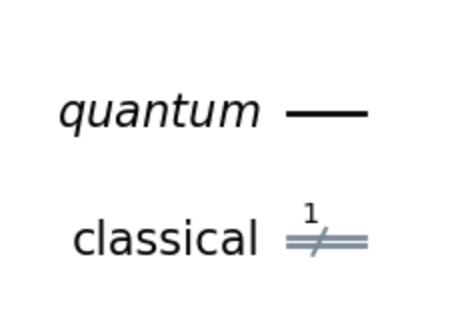
Here, you can see the quantum register and the classical register with no gates applied yet. Next, you can apply the Hadamard gate to the qubit. In Qiskit, this is done using the .h() method on the quantum circuit object. Here’s how you can do it:
quantum_circuit.py
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister
qr = QuantumRegister(1, name="quantum")
cr = ClassicalRegister(1, name="classical")
qc = QuantumCircuit(qr, cr)
qc.h(0)
qc.draw("mpl", filename="quantum_circuit.png")
Here, you’re applying the Hadamard gate to the first qubit in the quantum register. Since your circuit could have more than one qubit, you need to specify which qubit you’d like the gate to be applied to. Here, you have one qubit at index 0, which is why you specified qc.h(0). After applying the gate, you can visualize the circuit again using the .draw() method. The output should now show the Hadamard gate applied to your qubit:
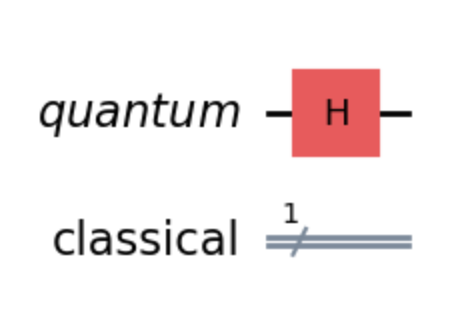
Now, the qubit is in a superposition state. To see the effect of this, you need to measure the qubit and store the result in the classical bit. In Qiskit, you can do this using the .measure() method on the quantum circuit object. Here’s how you can add the measurement step:
quantum_circuit.py
from qiskit import ClassicalRegister, QuantumCircuit, QuantumRegister
qr = QuantumRegister(1, name="quantum")
cr = ClassicalRegister(1, name="classical")
qc = QuantumCircuit(qr, cr)
qc.h(0)
qc.measure(0, 0)
qc.draw("mpl", filename="quantum_circuit.png")
You’ve measured the first qubit and stored the result in the first classical bit. Visualizing the circuit again, you should see the measurement operation added to the circuit:
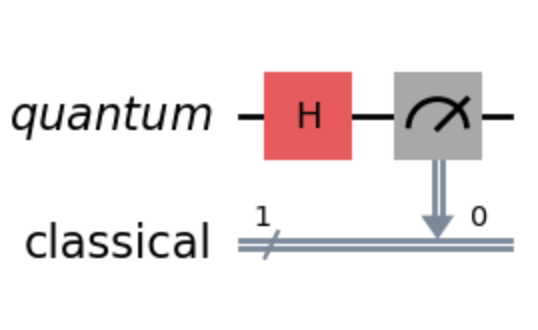
This is your complete quantum circuit that puts a qubit into superposition and then measures it. If you run this circuit ten thousand times, then you’ll get a histogram like this:
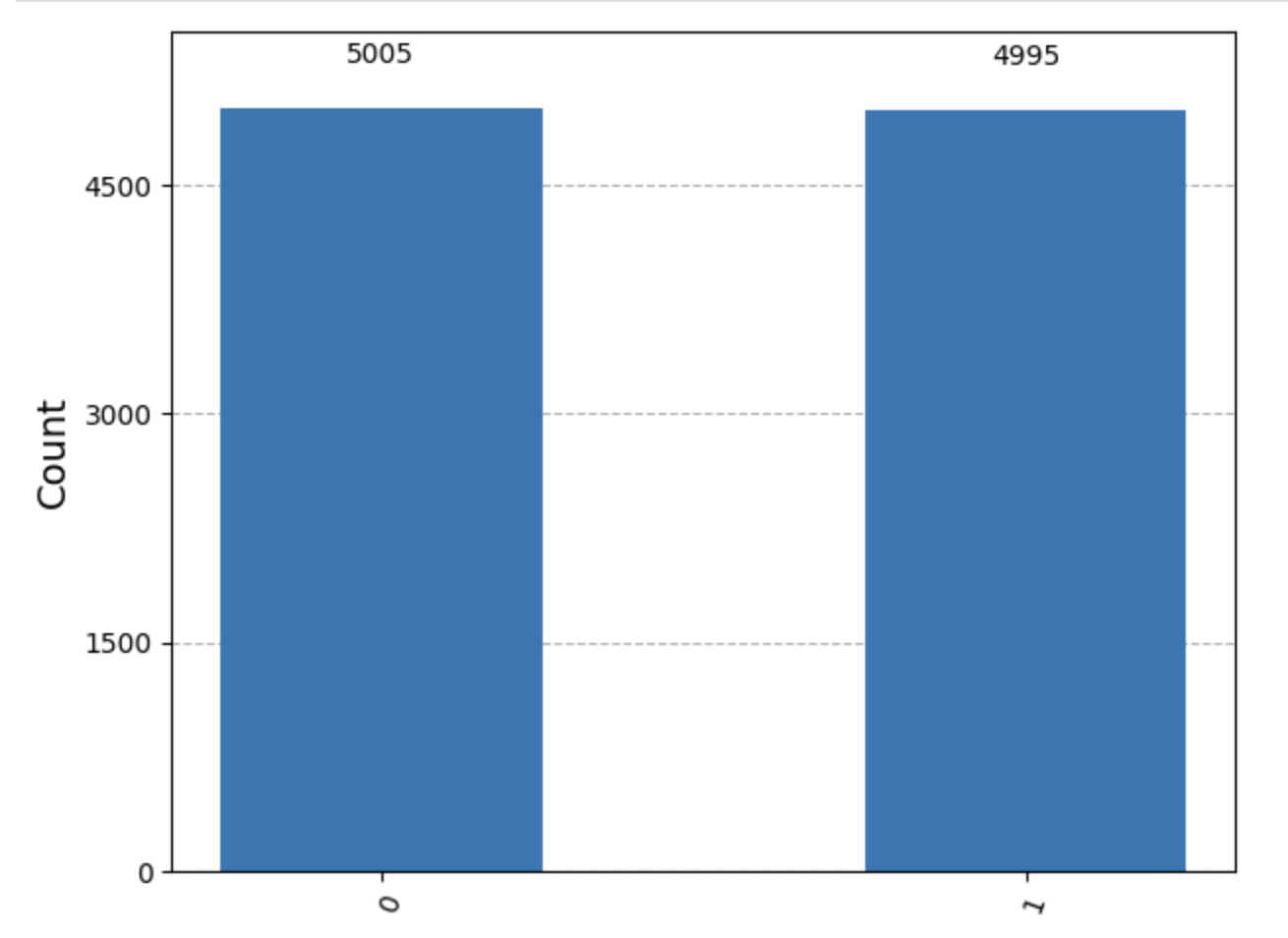
The results are roughly evenly split between 0 and 1, showing you superposition in action. The qubit existed in both states simultaneously, and after measurement, it collapsed to either 0 or 1 with approximately equal probability.
To keep the focus on fundamentals and circuit composition, this tutorial doesn’t walk through the full simulation and plotting code used to generate the measurement histogram.
To see how to go from a circuit to running shots and plotting a histogram, check out the official IBM Quantum docs on Qiskit Patterns.
Next Steps to Build on Quantum Computing Basics
You designed a one-qubit quantum circuit using Qiskit. Now, you’re ready to move on to actually running your circuits on simulators and real quantum hardware. To do that, you need to set up an IBM Quantum account and follow their tutorial on how to get started.
Quantum work requires linear algebra. Important topics to review are eigenvalues and eigenvectors, and tensor products. Studying linear algebra will serve you well as you dive further into the world of quantum computing.
Conclusion
Great job! You just learned the basics of quantum computing, one of the most exciting yet counterintuitive fields.
You learned that quantum mechanics offers new ways to process information that go beyond classical limits. Here are the key concepts you explored:
- Qubits are the building blocks of quantum information. They can be 0, 1, or both at once in a superposition, which lets quantum computers explore many possibilities in parallel.
- Measurement turns a qubit’s uncertain state into a definite 0 or 1, removing the superposition.
- Entanglement links qubits so that a change in one affects the other instantly, even across large distances.
- Interference shapes how these states combine, helping algorithms strengthen the right answers and suppress the wrong ones.
You first saw how the core ideas of superposition, entanglement, and interference show up inside real quantum algorithms like Shor’s and Grover’s, where they provide speedups over classical methods. After that, you coded a quantum circuit in Qiskit and watched how individual quantum gates transform a qubit step by step.
Quantum computing is still in its early stages, but by experimenting with real qubits on today’s NISQ devices using tools like Qiskit, you’re preparing for a future where advancing hardware and algorithms could make true quantum advantage possible.
Get Your Code: Click here to download the free sample code to build a quantum circuit with Qiskit.
Frequently Asked Questions
Now that you have some experience with quantum computing basics in Python, you can use the questions and answers below to check your understanding and recap what you’ve learned.
These FAQs are related to the most important concepts you’ve covered in this tutorial. Click the Show/Hide toggle beside each question to reveal the answer.
You treat a classical bit as 0 or 1, while you prepare a qubit in a superposition that weights 0 and 1 at the same time. You only see a definite 0 or 1 after measurement.
You collapse the qubit to 0 or 1, with probabilities given by amplitudes squared. You repeat many shots to observe the expected frequency.
You build a QuantumCircuit() with one qubit and call .h() on that qubit to apply a Hadamard gate. You then call .measure() to record the outcome in a classical bit.
You entangle qubits to create strong correlations that reveal structure when you measure. You use interference to cancel wrong paths and boost right ones, which lets you read useful patterns more efficiently.
Noisy intermediate-scale quantum (NISQ) devices encounter decoherence, noise, and complexity as you scale qubits, which introduces errors and short circuit depths. So, you often rely on hybrid workflows that combine quantum runs with classical postprocessing.
Take the Quiz: Test your knowledge with our interactive “Quantum Computing Basics With Qiskit” quiz. You’ll receive a score upon completion to help you track your learning progress:
Interactive Quiz
Quantum Computing Basics With QiskitTest your understanding of quantum computing basics, including superposition, qubits, entanglement, and key programming concepts.