Intermediate Python Tutorials
Once you’re past the basics you can start digging into our intermediate-level tutorials that will teach you new Python concepts. This category is for intermediate Python developers who already know the basics of Python development and want to expand their knowledge.
If you are new to Python, we suggest you start with our Python Basics category, which takes you on a comprehensive tour through the Python language and related concepts, even if you are a complete beginner.
Becoming a Python expert takes time, but over time you’ll master this beautiful programming language. It’s worth it! When you’re ready to move on to more difficult topics, check out our Advanced Python Tutorials section.
Free Bonus: 5 Thoughts On Python Mastery, a free course for Python developers that shows you the roadmap and the mindset you’ll need to take your Python skills to the next level.
Control Flow Structures in Python
May 28, 2025 intermediate python
Control Flow Structures in Python
May 28, 2025 intermediate python
The LEGB Rule & Understanding Python Scope
May 27, 2025 intermediate python
First Steps With LangChain
May 20, 2025 intermediate databases data-science
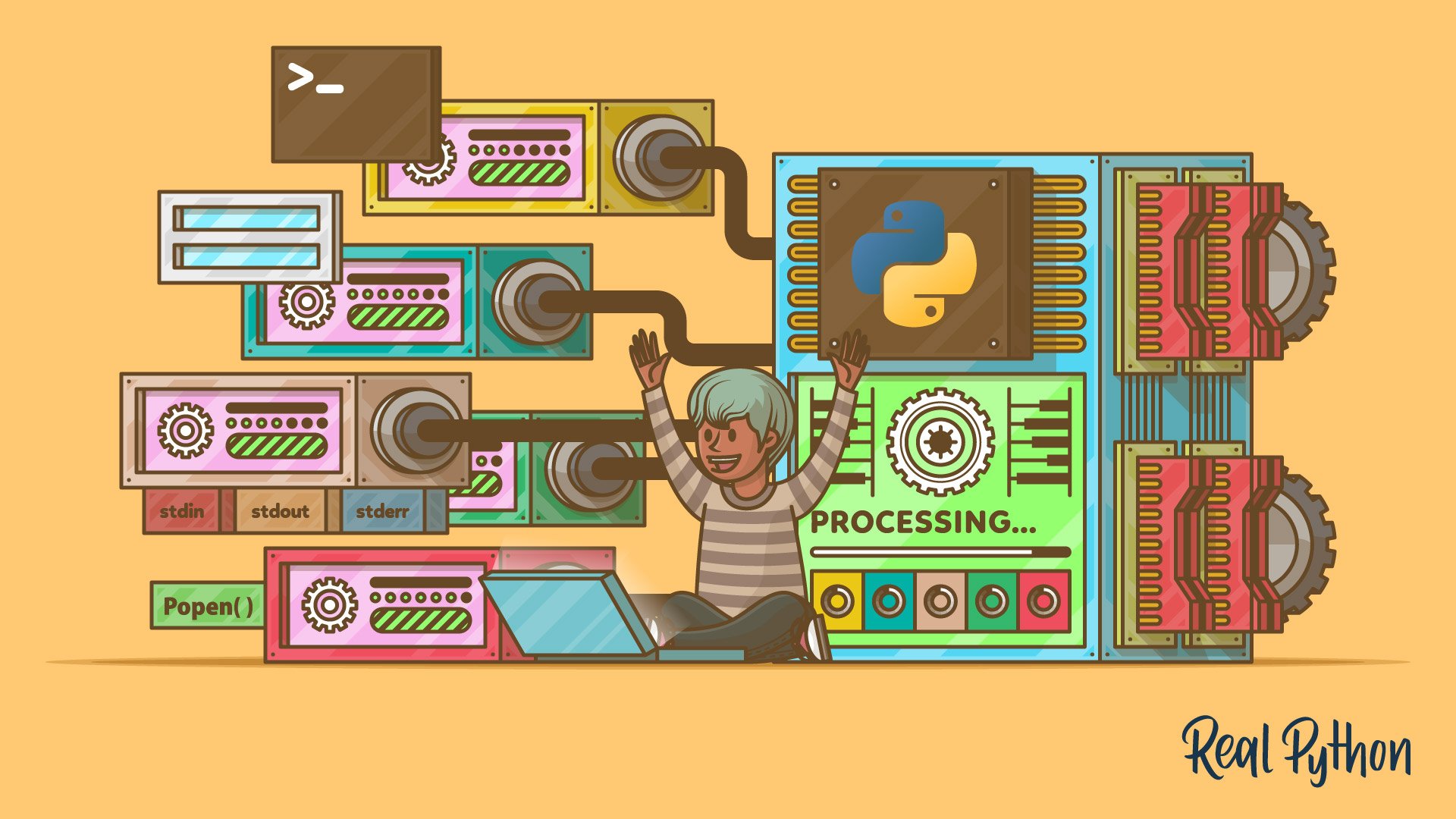
Using the Python subprocess Module
May 06, 2025 intermediate
Python Logging With the Loguru Library
May 06, 2025 intermediate tools
MySQL Databases and Python
Apr 22, 2025 intermediate databases data-science
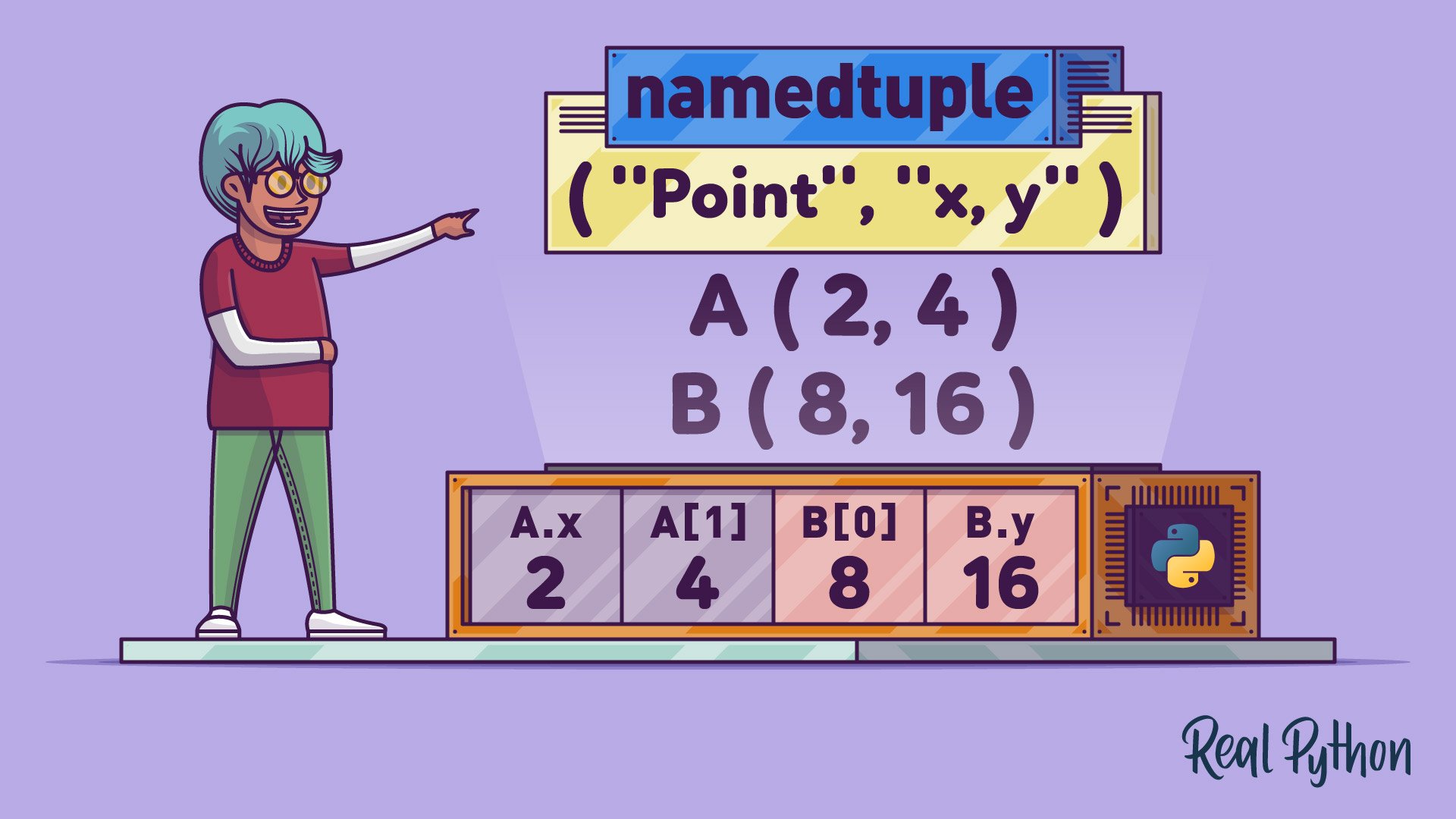
Namespaces in Python
Apr 14, 2025 intermediate python
Introducing DuckDB
Mar 26, 2025 intermediate databases data-science python
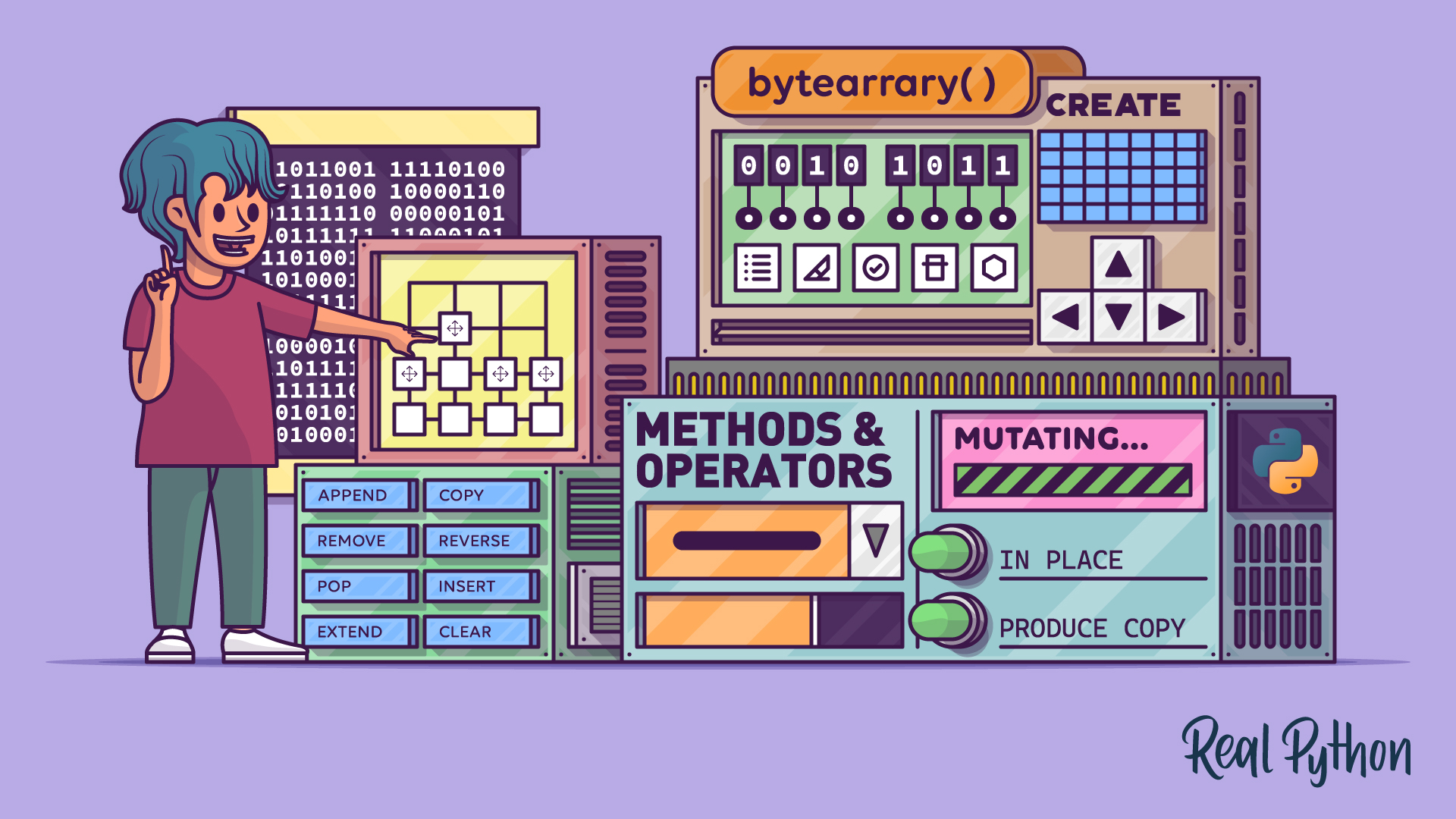
Python's Bytearray
Mar 19, 2025 intermediate python
Introducing DuckDB
Mar 17, 2025 intermediate databases data-science python
Getting to Know Duck Typing in Python
Mar 11, 2025 intermediate python