Learn how to work with absolute values in Python using the built-in abs() function for numbers, arrays, and custom objects. This tutorial shows you how to implement the absolute value function from scratch, use abs() with numbers, and customize its behavior for data types like NumPy arrays and pandas Series.
By the end of this tutorial, you’ll understand that:
- You can implement the absolute value function in Python using conditional statements or mathematical operations.
- Python’s built-in
abs()function efficiently handles integers, floating-point numbers, complex numbers, and more. - NumPy and pandas extend the
abs()function to work directly with arrays and Series. - You can customize the behavior of
abs()for your own data types by implementing the.__abs__()method. - The
abs()function can process fractions and decimals from Python’s standard library.
Don’t worry if your mathematical knowledge of the absolute value function is a little rusty. You’ll begin by refreshing your memory before diving deeper into Python code. That said, feel free to skip the next section and jump right into the nitty-gritty details that follow.
Get Your Code: Click here to download the free sample code that you’ll use to find absolute values in Python.
Take the Quiz: Test your knowledge with our interactive “How to Find an Absolute Value in Python” quiz. You’ll receive a score upon completion to help you track your learning progress:
Interactive Quiz
How to Find an Absolute Value in PythonIn this quiz, you'll test your knowledge of calculating absolute values in Python, mastering both built-in functions and common use cases to improve your coding accuracy.
Defining the Absolute Value
The absolute value lets you determine the size or magnitude of an object, such as a number or a vector, regardless of its direction. Real numbers can have one of two directions when you ignore zero: they can be either positive or negative. On the other hand, complex numbers and vectors can have many more directions.
Note: When you take the absolute value of a number, you lose information about its sign or, more generally, its direction.
Consider a temperature measurement as an example. If the thermometer reads -12°C, then you can say it’s twelve degrees Celsius below freezing. Notice how you decomposed the temperature in the last sentence into a magnitude, twelve, and a sign. The phrase below freezing means the same as below zero degrees Celsius. The temperature’s size or absolute value is identical to the absolute value of the much warmer +12°C.
Using mathematical notation, you can define the absolute value of 𝑥 as a piecewise function, which behaves differently depending on the range of input values. A common symbol for absolute value consists of two vertical lines:
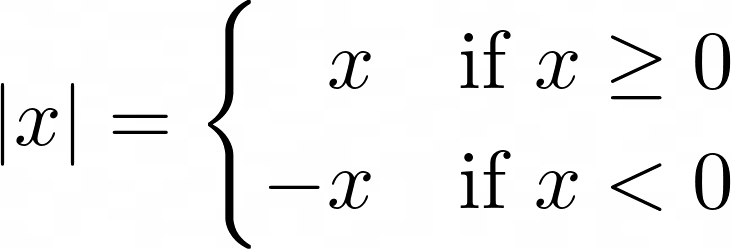
This function returns values greater than or equal to zero without alteration. On the other hand, values smaller than zero have their sign flipped from a minus to a plus. Algebraically, this is equivalent to taking the square root of a number squared:
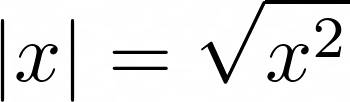
When you square a real number, you always get a positive result, even if the number that you started with was negative. For example, the square of -12 and the square of 12 have the same value, equal to 144. Later, when you compute the square root of 144, you’ll only get 12 without the minus sign.
Geometrically, you can think of an absolute value as the distance from the origin, which is zero on a number line in the case of the temperature reading from before:
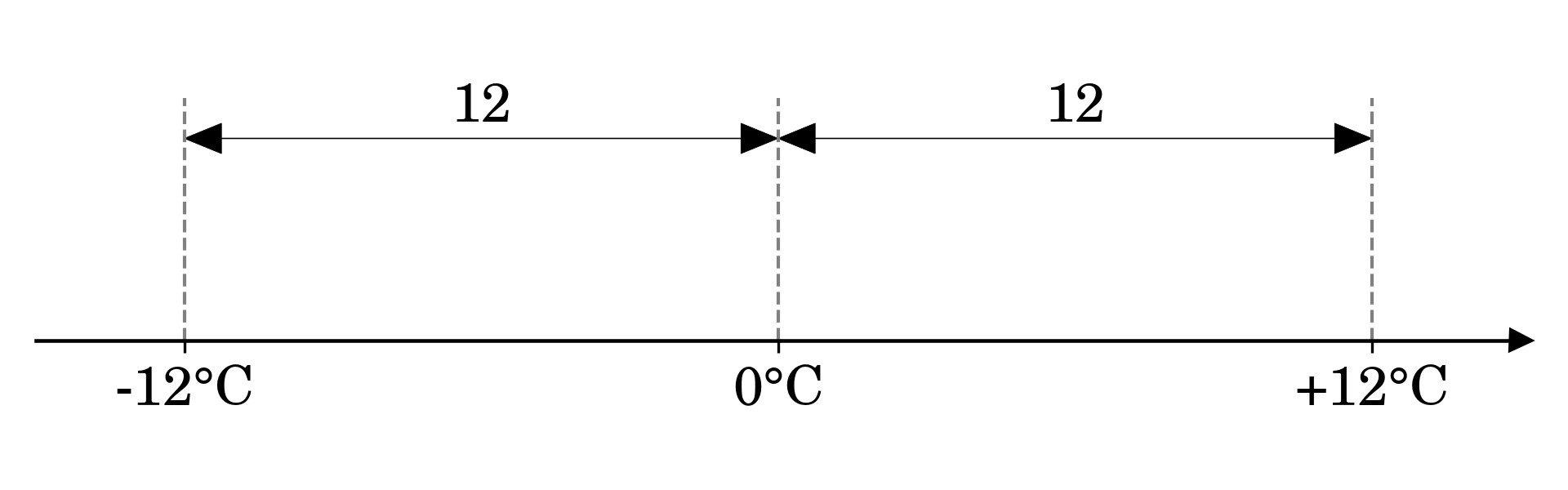
To calculate this distance, you can subtract the origin from the temperature reading (-12°C - 0°C = -12°C) or the other way around (0°C - (-12°C) = +12°C), and then drop the sign of the result. Subtracting zero doesn’t make much difference here, but the reference point may sometimes be shifted. That’s the case for vectors bound to a fixed point in space, which becomes their origin.
Vectors, just like numbers, convey information about the direction and the magnitude of a physical quantity, but in more than one dimension. For example, you can express the velocity of a falling snowflake as a three-dimensional vector:
This vector indicates the snowflake’s current position relative to the origin of the coordinate system. It also shows the snowflake’s direction and pace of motion through the space. The longer the vector, the greater the magnitude of the snowflake’s speed. As long as the coordinates of the vector’s initial and terminal points are expressed in meters, calculating its length will get you the snowflake’s speed measured in meters per unit of time.
Note: There are two ways to look at a vector. A bound vector is an ordered pair of fixed points in space, whereas a free vector only tells you about the displacement of the coordinates from point A to point B without revealing their absolute locations. Consider the following code snippet as an example:
>>> A = [1, 2, 3]
>>> B = [3, 2, 1]
>>> bound_vector = [A, B]
>>> bound_vector
[[1, 2, 3], [3, 2, 1]]
>>> free_vector = [b - a for a, b in zip(A, B)]
>>> free_vector
[2, 0, -2]
A bound vector wraps both points, providing quite a bit of information. In contrast, a free vector only represents the shift from A to B. You can calculate a free vector by subtracting the initial point, A, from the terminal one, B. One way to do so is by iterating over the consecutive pairs of coordinates with a list comprehension.
A free vector is essentially a bound vector translated to the origin of the coordinate system, so it begins at zero.
The length of a vector, also known as its magnitude, is the distance between its initial and terminal points, 𝐴 and 𝐵, which you can calculate using the Euclidean norm:
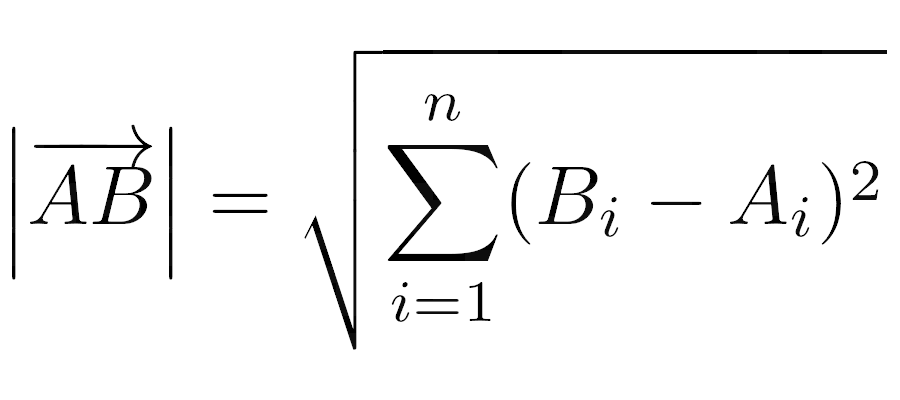
This formula calculates the length of the 𝑛-dimensional vector 𝐴𝐵, by summing the squares of the differences between the coordinates of points 𝐴 and 𝐵 in each dimension indexed by 𝑖. For a free vector, the initial point, 𝐴, becomes the origin of the coordinate system—or zero—which simplifies the formula, as you only need to square the coordinates of your vector.
Recall the algebraic definition of an absolute value. For numbers, it was the square root of a number squared. Now, when you add more dimensions to the equation, you end up with the formula for the Euclidean norm, shown above. So, the absolute value of a vector is equivalent to its length!
All right. Now that you know when absolute values might be useful, it’s time to implement them in Python!
Implementing the Absolute Value Function in Python
To implement the absolute value function in Python, you can take one of the earlier mathematical definitions and translate it into code. For instance, the piecewise function may look like this:
def absolute_value(x):
if x >= 0:
return x
else:
return -x
You use a conditional statement to check whether the given number denoted with the letter x is greater than or equal to zero. If so, then you return the same number. Otherwise, you flip the number’s sign. Because there are only two possible outcomes here, you can rewrite the above function using a conditional expression that comfortably fits on a single line:
def absolute_value(x):
return x if x >= 0 else -x
It’s exactly the same behavior as before, only implemented in a slightly more compact way. Conditional expressions are useful when you don’t have a lot of logic that goes into the two alternative branches in your code.
Note: Alternatively, you can write this even more concisely by relying on Python’s built-in max() function, which returns the largest argument:
def absolute_value(x):
return max(x, -x)
If the number 𝑥 is negative, then this function will return its positive value. Otherwise, it’ll return 𝑥 itself.
The algebraic definition of an absolute value is also pretty straightforward to implement in Python:
from math import sqrt
def absolute_value(x):
return sqrt(pow(x, 2))
First, you import the square root function from the math module and then call it on the given number raised to the power of two. The power function is built right into Python, so you don’t have to import it. Alternatively, you can avoid the import statement altogether by leveraging Python’s exponentiation operator (**), which can simulate the square root function:
def absolute_value(x):
return (x**2) ** 0.5
This is sort of a mathematical trick because using a fractional exponent is equivalent to computing the 𝑛th root of a number. In this case, you take a squared number to the power of one-half (0.5) or one over two (½), which is the same as calculating the square root. Note that both Python implementations based on the algebraic definition suffer from a slight deficiency:
>>> def absolute_value(x):
... return (x**2) ** 0.5
>>> absolute_value(-12)
12.0
>>> type(12.0)
<class 'float'>
You always end up with a floating-point number, even if you started with an integer. So, if you’d like to preserve the original data type of a number, then you might prefer the piecewise-based implementation instead.
As long as you stay within integers and floating-point numbers, you can also write a somewhat silly implementation of the absolute value function by leveraging the textual representation of numbers in Python:
def absolute_value(x):
return float(str(x).lstrip("-"))
You convert the function’s argument, x, to a Python string using the built-in str() function. This lets you strip the leading minus sign, if there is one, with an empty string. Then, you convert the result to a floating-point number with float(). Note this implementation always converts integers to floats.
Implementing the absolute value function from scratch in Python is a worthwhile learning exercise. However, in real-life applications, you should take advantage of the built-in abs() function that comes with Python. You’ll find out why in the next section.
Using the Built-in abs() Function With Numbers
The last function that you implemented above was probably the least efficient one because of the data conversions and the string operations, which are usually slower than direct number manipulation. But in truth, all of your hand-made implementations of an absolute value pale in comparison to the abs() function that’s built into the language. That’s because abs() is compiled to blazing-fast machine code, while your pure-Python code isn’t.
You should always prefer abs() over your custom functions. It runs much more quickly, an advantage that can really add up when you have a lot of data to process. Additionally, it’s much more versatile, as you’re about to find out.
Integers and Floating-Point Numbers
The abs() function is one of the built-in functions that are part of the Python language. That means you can start using it right away without importing:
>>> abs(-12)
12
>>> abs(-12.0)
12.0
As you can see, abs() preserves the original data type. In the first case, you passed an integer literal and got an integer result. When called with a floating-point number, the function returned a Python float. But these two data types aren’t the only ones that you can call abs() on. The third numeric type that abs() knows how to handle is Python’s complex data type, which represents complex numbers.
Complex Numbers
You can think of a complex number as a pair consisting of two floating-point values, commonly known as the real part and the imaginary part. One way to define a complex number in Python is by calling the built-in complex() function:
>>> z = complex(3, 2)
It accepts two arguments. The first one represents the real part, while the second one represents the imaginary part. At any point, you can access the complex number’s .real and .imag attributes to get those parts back:
>>> z.real
3.0
>>> z.imag
2.0
Both of them are read-only and are always expressed as floating-point values. Also, the absolute value of a complex number returned by abs() happens to be a floating-point number:
>>> abs(z)
3.605551275463989
This might surprise you until you find out that complex numbers have a visual representation that resembles two-dimensional vectors fixed at the coordinate system’s origin:
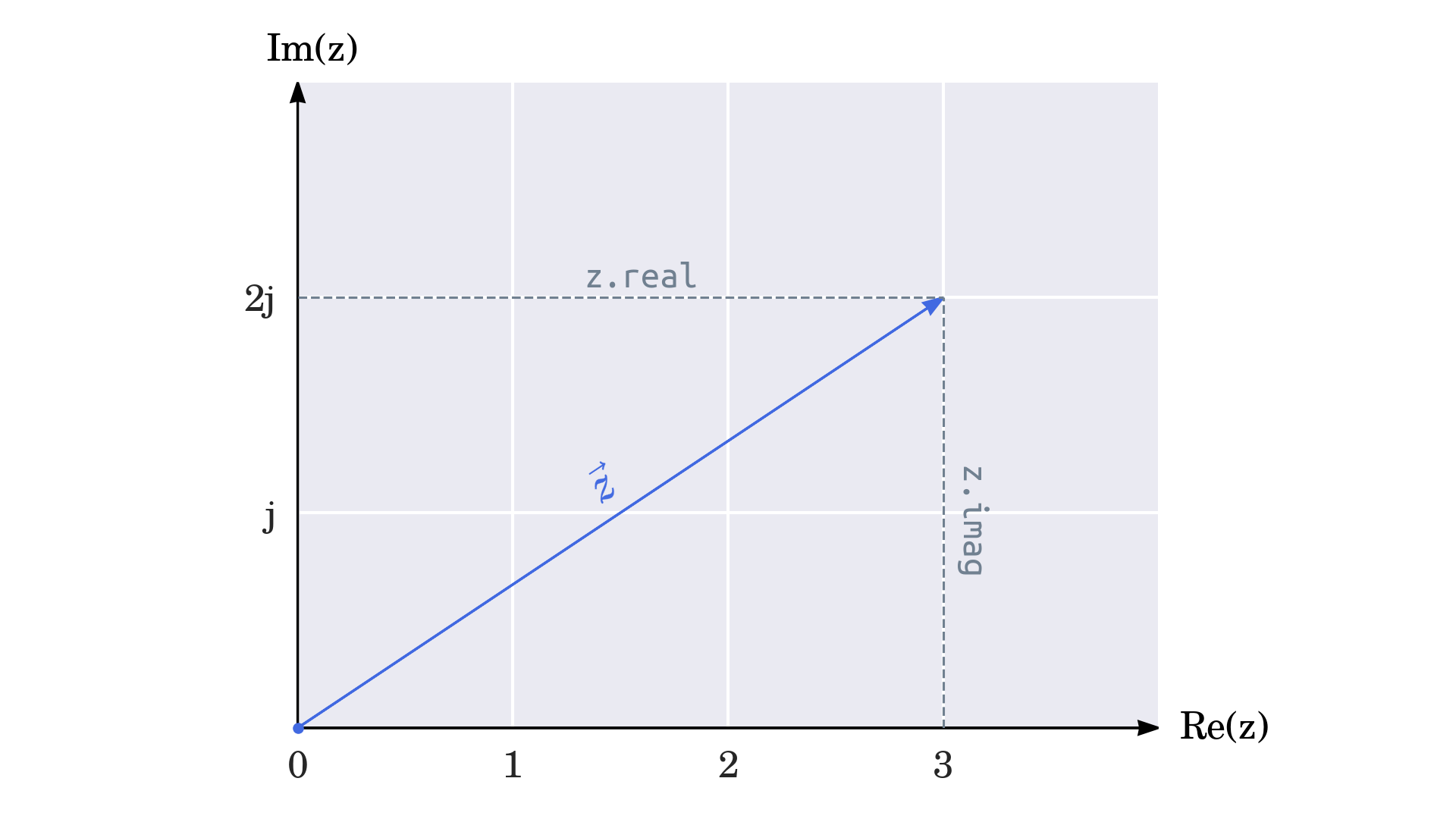
You already know the formula to calculate the length of such a vector, which in this case agrees with the number returned by abs(). Note that the absolute value of a complex number is more commonly referred to as the magnitude, modulus, or radius of a complex number.
While integers, floating-point numbers, and complex numbers are the only numeric types supported natively by Python, you’ll find two additional numeric types in its standard library. They, too, can interoperate with the abs() function.
Fractions and Decimals
The abs() function in Python accepts all numeric data types available, including the lesser-known fractions and decimals. For instance, you can get the absolute value of one-third or minus three-quarters defined as Fraction instances:
>>> from fractions import Fraction
>>> abs(Fraction("1/3"))
Fraction(1, 3)
>>> abs(Fraction("-3/4"))
Fraction(3, 4)
In both cases, you get another Fraction object back, but it’s unsigned. That can be convenient if you plan to continue your computations on fractions, which offer higher precision than floating-point numbers.
If you’re working in finance, then you’ll probably want to use Decimal objects to help mitigate the floating-point representation error. Luckily, you can take the absolute value of these objects:
>>> from decimal import Decimal
>>> abs(Decimal("0.3333333333333333"))
Decimal('0.3333333333333333')
>>> abs(Decimal("-0.75"))
Decimal('0.75')
Again, the abs() function conveniently returns the same data type as the one that you supplied, but it gives you an appropriate positive value.
Wow, abs() can deal with an impressive variety of numeric data types! But it turns out that abs() is even more clever than that. You can even call it on some objects delivered by third-party libraries, as you’ll try out in the next section.
Calling abs() on Other Python Objects
Say you want to compute the absolute values of average daily temperature readings over some period. Unfortunately, as soon as you try calling abs() on a Python list with those numbers, you get an error:
>>> temperature_readings = [1, -5, 1, -4, -1, -8, 0, -7, 3, -5, 2]
>>> abs(temperature_readings)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: bad operand type for abs(): 'list'
That’s because abs() doesn’t know how to process a list of numbers. To work around this, you could use a list comprehension or call Python’s map() function, like so:
>>> [abs(x) for x in temperature_readings]
[1, 5, 1, 4, 1, 8, 0, 7, 3, 5, 2]
>>> list(map(abs, temperature_readings))
[1, 5, 1, 4, 1, 8, 0, 7, 3, 5, 2]
Both implementations do the job but require an additional step, which may not always be desirable. If you want to cut that extra step, then you may look into external libraries that change the behavior of abs() for your convenience. That’s what you’ll explore below.
NumPy Arrays and pandas Series
One of the most popular libraries for extending Python with high-performance arrays and matrices is NumPy. Its 𝑛-dimensional array data structure, ndarray, is the cornerstone of numerical computing in Python, so many other libraries use it as a foundation.
Once you convert a regular Python list to a NumPy array with np.array(), you’ll be able to call some of the built-in functions, including abs(), on the result:
>>> import numpy as np
>>> temperature_readings = np.array([1, -5, 1, -4, -1, -8, 0, -7, 3, -5, 2])
>>> abs(temperature_readings)
array([1, 5, 1, 4, 1, 8, 0, 7, 3, 5, 2])
In response to calling abs() on a NumPy array, you get another array with the absolute values of the original elements. It’s as if you iterated over the list of temperature readings yourself and applied the abs() function on each element individually, just as you did with a list comprehension before.
You can convert a NumPy array back to a Python list if you find that more suitable:
>>> list(abs(temperature_readings))
[1, 5, 1, 4, 1, 8, 0, 7, 3, 5, 2]
However, note that NumPy arrays share most of the Python list interface. For example, they support indexing and slicing, and their methods are similar to those of plain lists, so most people usually just stick to using NumPy arrays without ever looking back at lists.
pandas is another third-party library widely used in data analysis thanks to its Series and DataFrame objects. A Series is a sequence of observations or a column, whereas a DataFrame is like a table or a collection of columns. You can call abs() on both of them.
Suppose you have a Python dictionary that maps a city name to its lowest average temperatures observed monthly over the course of a year:
>>> lowest_temperatures = {
... "Reykjav\xedk": [-3, -2, -2, 1, 4, 7, 9, 8, 6, 2, -1, -2],
... "Rovaniemi": [-16, -14, -10, -3, 3, 8, 12, 9, 5, -1, -6, -11],
... "Valetta": [9, 9, 10, 12, 15, 19, 21, 22, 20, 17, 14, 11],
... }
Each city has twelve temperature readings, spanning from January to December. Now, you can turn that dictionary into a pandas DataFrame object so that you can draw some interesting insights going forward:
>>> import calendar
>>> import pandas as pd
>>> df = pd.DataFrame(lowest_temperatures, index=calendar.month_abbr[1:])
>>> df
Reykjavík Rovaniemi Valetta
Jan -3 -16 9
Feb -2 -14 9
Mar -2 -10 10
Apr 1 -3 12
May 4 3 15
Jun 7 8 19
Jul 9 12 21
Aug 8 9 22
Sep 6 5 20
Oct 2 -1 17
Nov -1 -6 14
Dec -2 -11 11
Instead of using the default zero-based index, your DataFrame is indexed by abbreviated month names, which you obtained with the help of the calendar module. Each column in the DataFrame has a sequence of temperatures from the original dictionary, represented as a Series object:
>>> df["Rovaniemi"]
Jan -16
Feb -14
Mar -10
Apr -3
May 3
Jun 8
Jul 12
Aug 9
Sep 5
Oct -1
Nov -6
Dec -11
Name: Rovaniemi, dtype: int64
>>> type(df["Rovaniemi"])
<class 'pandas.core.series.Series'>
By using the square bracket ([]) syntax and a city name like Rovaniemi, you can extract a single Series object from the DataFrame and narrow down the amount of information displayed.
pandas, just like NumPy, lets you call many of Python’s built-in functions on its objects, including its DataFrame and Series objects. Specifically, you can call abs() to calculate more than one absolute value in one go:
>>> abs(df)
Reykjavík Rovaniemi Valetta
Jan 3 16 9
Feb 2 14 9
Mar 2 10 10
Apr 1 3 12
May 4 3 15
Jun 7 8 19
Jul 9 12 21
Aug 8 9 22
Sep 6 5 20
Oct 2 1 17
Nov 1 6 14
Dec 2 11 11
>>> abs(df["Rovaniemi"])
Jan 16
Feb 14
Mar 10
Apr 3
May 3
Jun 8
Jul 12
Aug 9
Sep 5
Oct 1
Nov 6
Dec 11
Name: Rovaniemi, dtype: int64
Calling abs() on the entire DataFrame applies the function to each element in every column. You can also call abs() on the individual column.
How did NumPy and pandas change the behavior of Python’s built-in abs() function without modifying its underlying code? Well, it was possible because the function was designed with such extensions in mind. If you’re looking for an advanced use of abs(), then read on to make your own data type that’ll play nicely with that function.
Your Very Own Data Types
Depending on the data type, Python will handle the computation of absolute values differently.
When you call abs() on an integer, it’ll use a custom code snippet that resembles your piecewise function. However, that function will be implemented in the C programming language for efficiency. If you pass a floating-point number, then Python will delegate that call to C’s fabs() function. In the case of a complex number, it’ll call the hypot() function instead.
What about container objects like DataFrames, Series, and arrays?
Understandably, when you define a new data type in Python, it won’t work with the abs() function because its default behavior is unknown. However, you can optionally customize the behavior of abs() against the instances of your class by implementing the special .__abs__() method using pure Python. There’s a finite set of predefined special methods in Python that let you override how certain functions and operators should work.
Consider the following class representing a free 𝑛-dimensional vector in the Euclidean space:
>>> import math
>>> class Vector:
... def __init__(self, *coordinates):
... self.coordinates = coordinates
...
... def __abs__(self):
... origin = [0] * len(self.coordinates)
... return math.dist(origin, self.coordinates)
This class accepts one or more coordinate values, describing the displacement in each dimension from the origin of the coordinate system. Your special .__abs__() method calculates the distance from the origin, according to the Euclidean norm definition that you learned at the beginning of this tutorial.
To test your new class, you can create a three-dimensional velocity vector of a falling snowflake, for example, which might look like this:
>>> snowflake_velocity = Vector(0.42, 1.5, 0.87)
>>> abs(snowflake_velocity)
1.7841804841439108
Notice how calling abs() on your Vector class instance returns the correct absolute value, equal to about 1.78. The speed units will be expressed in meters per second as long as the snowflake’s displacement was measured in meters at two distinct time instants one second apart. In other words, it would take one second for the snowflake to travel from point A to point B.
Using the mentioned formula forces you to define the origin point. However, because your Vector class represents a free vector rather than a bound one, you can simplify your code by calculating the multidimensional hypotenuse using Python’s math.hypot() function:
>>> import math
>>> class Vector:
... def __init__(self, *coordinates):
... self.coordinates = coordinates
...
... def __abs__(self):
... return math.hypot(*self.coordinates)
>>> snowflake_velocity = Vector(0.42, 1.5, 0.87)
>>> abs(snowflake_velocity)
1.7841804841439108
You get the same result with fewer lines of code. Note that hypot() is a variadic function accepting a variable number of arguments, so you must use the star operator (*) to unpack your tuple of coordinates into those arguments.
Awesome! You can now implement your own library, and Python’s built-in abs() function will know how to work with it. That gives you functionality similar to what you get working with NumPy or pandas!
Conclusion
Implementing formulas for an absolute value in Python is a breeze. However, Python already comes with the versatile abs() function, which lets you calculate the absolute value of various types of numbers, including integers, floating-point numbers, complex numbers, and more. You can also use abs() on instances of custom classes and third-party library objects.
In this tutorial, you learned how to:
- Implement the absolute value function from scratch
- Use the built-in
abs()function in Python - Calculate absolute values for numbers
- Call
abs()on NumPy arrays and pandas Series - Customize the behavior of
abs()on objects
With this knowledge, you’re now equipped with an effective tool for calculating absolute values in Python.
Get Your Code: Click here to download the free sample code that you’ll use to find absolute values in Python.
Frequently Asked Questions
Now that you have some experience with absolute values in Python, you can use the questions and answers below to check your understanding and recap what you’ve learned.
These FAQs are related to the most important concepts you’ve covered in this tutorial. Click the Show/Hide toggle beside each question to reveal the answer.
You can find the absolute value of a number in Python by using the built-in abs() function, which returns the magnitude of the number regardless of its sign.
Yes, you can find the absolute value of a complex number in Python using the abs() function. This function calculates the magnitude of the complex number as a floating-point value.
To calculate the absolute value of a list of numbers in Python, you can use a list comprehension or the map() function to apply abs() to each element in the list.
You customize the behavior of abs() for a custom class by defining the .__abs__() method within the class, which allows you to specify how the absolute value should be calculated for instances of that class.
Take the Quiz: Test your knowledge with our interactive “How to Find an Absolute Value in Python” quiz. You’ll receive a score upon completion to help you track your learning progress:
Interactive Quiz
How to Find an Absolute Value in PythonIn this quiz, you'll test your knowledge of calculating absolute values in Python, mastering both built-in functions and common use cases to improve your coding accuracy.