The Python Square Root Function

Square Roots in Mathematics

In algebra, a square, x, is the result of a number, n, multiplied by itself: x = n²

You can calculate squares using Python:

>>> n = 5
>>> x = n**2
>>> x
25

The Python ** operator is used for calculating the power of a number. In this case, 5 squared, or 5 to the power of 2, is 25.

The square root, then, is the number n, which when multiplied by itself yields the square, x.

In this example, n, the square root of 25, is 5.

25 is an example of a perfect square. Perfect squares are the squares of integer values:

>>> 1**2
1

>>> 2**2
4

>>> 3**2
9

You might have memorized some of these perfect squares when you learned your multiplication tables in an elementary algebra class.

If you’re given a small perfect square, it may be straightforward enough to calculate or memorize its square root. But for most other squares, this calculation can get a bit more tedious. Often, an estimation is good enough when you don’t have a calculator.

Fortunately, as a Python developer, you do have a calculator, namely the Python interpreter!

The Python Square Root Function

Python’s math module in the standard library can help you work on math-related problems in code. It contains many useful functions, such as remainder() and factorial(). It also includes the Python square root function, sqrt().

You’ll begin by importing math:

>>> import math

That’s all it takes! You can now use math.sqrt() to calculate square roots.

sqrt() has a straightforward interface. It takes one parameter, x, which as you saw before, stands for the square you want to calculate the square root for. In the example from earlier, this would be 25.

The return value of sqrt() is the square root of x, as a floating-point number. In the example, this would be 5.0.

Next, you’ll take a look at some examples of how to use sqrt() and how not to use sqrt().

>>> math.sqrt(49)
7.0

>>> math.sqrt(70.5)
8.396427811873332

>>> 8.396427811873332**2
70.5

>>> math.sqrt(0)
0.0

>>> math.sqrt(-25)
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: math domain error

Square Roots in the Real World

To see a real-world application of the Python square root function, you’ll turn to the sport of tennis.

Imagine that Alex de Minaur, one of the fastest players in the world, has just hit a forehand from the back corner, where the baseline meets the sideline of the tennis court:

Now, assume his opponent has countered with a drop shot—one that would place the ball short with little forward momentum—to the opposite corner, where the other sideline meets the net:

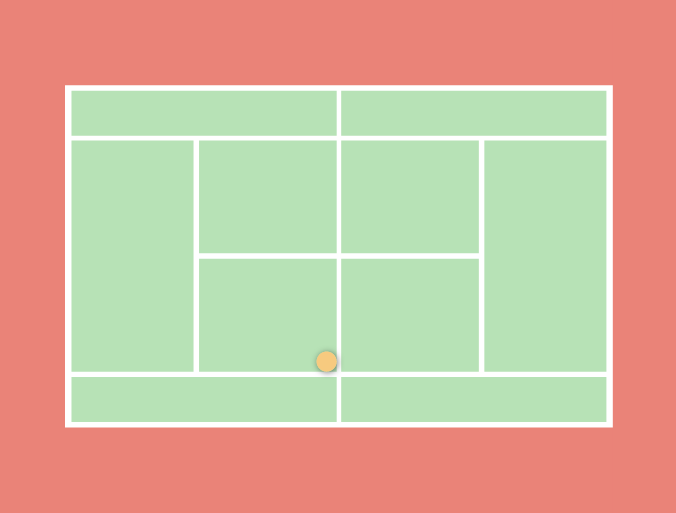
How far must Nadal run to reach the ball?

You can determine from regulation tennis court dimensions that the baseline is 27 feet long, and the sideline on one side of the net is 39 feet long. So, essentially, this boils down to solving for the hypotenuse of a right triangle:

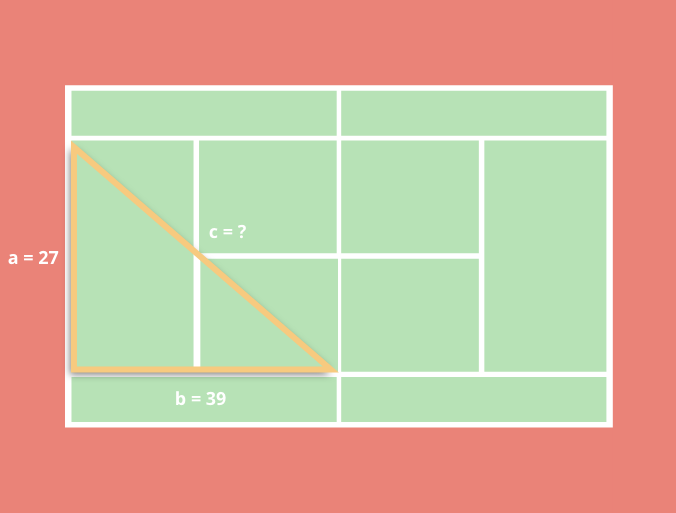
Using a valuable equation from geometry, the Pythagorean theorem, you know that a² + b² = c², where a and b are the legs of the right triangle and c is the hypotenuse.

Therefore, you can calculate the distance Nadal must run by rearranging the equation to solve for c:

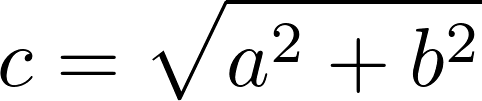
You can solve this equation using the Python square root function:

>>> a = 27
>>> b = 39
>>> math.sqrt(a**2 + b**2)
47.43416490252569

So, Nadal must run about 47.4 feet (14.5 meters) in order to reach the ball and save the point.

Conclusion

Congratulations! You now know all about the Python square root function.

In this tutorial, you’ve covered:

• A brief introduction to square roots
• The ins and outs of the Python square root function, sqrt()
• A practical application of sqrt() using a real-world example

Knowing how to use sqrt() is only part of the equation. Understanding when to use it is equally important. Now that you know both, go ahead and apply your newfound mastery of the Python square root function!

FAQs

You now have some experience with square roots in Python. Below, you’ll find a few questions and answers that sum up the most important concepts that you’ve covered in this tutorial.

You can use these questions to check your understanding or to recap and solidify what you’ve just learned. After each question, you’ll find a brief explanation hidden in a collapsible section. Click the Show/Hide toggle to reveal the answer.