Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Python Histogram Plotting: NumPy, Matplotlib, Pandas & Seaborn
In this tutorial, you’ll be equipped to make production-quality, presentation-ready Python histogram plots with a range of choices and features.
If you have introductory to intermediate knowledge in Python and statistics, then you can use this article as a one-stop shop for building and plotting histograms in Python using libraries from its scientific stack, including NumPy, Matplotlib, pandas, and Seaborn.
A histogram is a great tool for quickly assessing a probability distribution that is intuitively understood by almost any audience. Python offers a handful of different options for building and plotting histograms. Most people know a histogram by its graphical representation, which is similar to a bar graph:
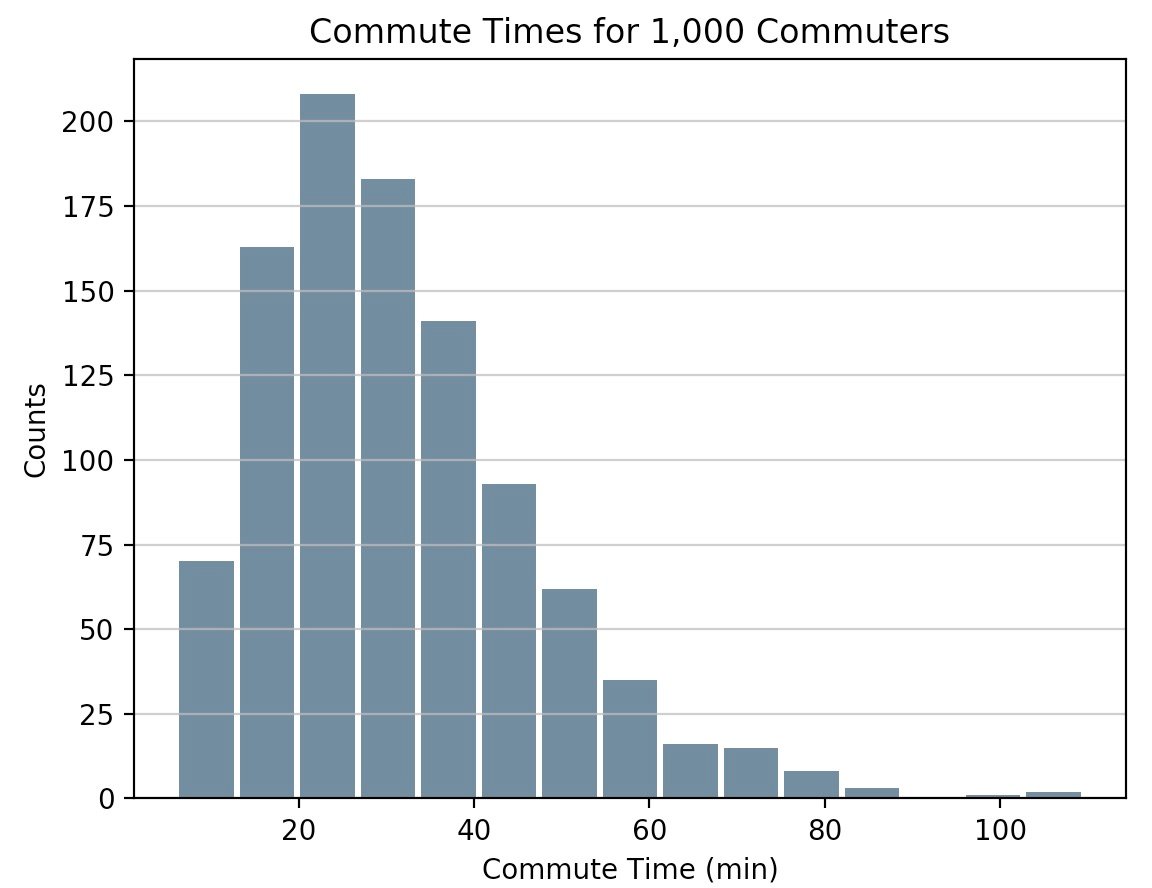
This article will guide you through creating plots like the one above as well as more complex ones. Here’s what you’ll cover:
- Building histograms in pure Python, without use of third party libraries
- Constructing histograms with NumPy to summarize the underlying data
- Plotting the resulting histogram with Matplotlib, pandas, and Seaborn
Free Bonus: Short on time? Click here to get access to a free two-page Python histograms cheat sheet that summarizes the techniques explained in this tutorial.
Histograms in Pure Python
When you are preparing to plot a histogram, it is simplest to not think in terms of bins but rather to report how many times each value appears (a frequency table). A Python dictionary is well-suited for this task:
>>> # Need not be sorted, necessarily
>>> a = (0, 1, 1, 1, 2, 3, 7, 7, 23)
>>> def count_elements(seq) -> dict:
... """Tally elements from `seq`."""
... hist = {}
... for i in seq:
... hist[i] = hist.get(i, 0) + 1
... return hist
>>> counted = count_elements(a)
>>> counted
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
count_elements() returns a dictionary with unique elements from the sequence as keys and their frequencies (counts) as values. Within the loop over seq, hist[i] = hist.get(i, 0) + 1 says, “for each element of the sequence, increment its corresponding value in hist by 1.”
In fact, this is precisely what is done by the collections.Counter class from Python’s standard library, which subclasses a Python dictionary and overrides its .update() method:
>>> from collections import Counter
>>> recounted = Counter(a)
>>> recounted
Counter({0: 1, 1: 3, 3: 1, 2: 1, 7: 2, 23: 1})
You can confirm that your handmade function does virtually the same thing as collections.Counter by testing for equality between the two:
>>> recounted.items() == counted.items()
True
Technical Detail: The mapping from count_elements() above defaults to a more highly optimized C function if it is available. Within the Python function count_elements(), one micro-optimization you could make is to declare get = hist.get before the for loop. This would bind a method to a variable for faster calls within the loop.
It can be helpful to build simplified functions from scratch as a first step to understanding more complex ones. Let’s further reinvent the wheel a bit with an ASCII histogram that takes advantage of Python’s output formatting:
def ascii_histogram(seq) -> None:
"""A horizontal frequency-table/histogram plot."""
counted = count_elements(seq)
for k in sorted(counted):
print('{0:5d} {1}'.format(k, '+' * counted[k]))
This function creates a sorted frequency plot where counts are represented as tallies of plus (+) symbols. Calling sorted() on a dictionary returns a sorted list of its keys, and then you access the corresponding value for each with counted[k]. To see this in action, you can create a slightly larger dataset with Python’s random module:
>>> # No NumPy ... yet
>>> import random
>>> random.seed(1)
>>> vals = [1, 3, 4, 6, 8, 9, 10]
>>> # Each number in `vals` will occur between 5 and 15 times.
>>> freq = (random.randint(5, 15) for _ in vals)
>>> data = []
>>> for f, v in zip(freq, vals):
... data.extend([v] * f)
>>> ascii_histogram(data)
1 +++++++
3 ++++++++++++++
4 ++++++
6 +++++++++
8 ++++++
9 ++++++++++++
10 ++++++++++++
Here, you’re simulating plucking from vals with frequencies given by freq (a generator expression). The resulting sample data repeats each value from vals a certain number of times between 5 and 15.
Note: random.seed() is use to seed, or initialize, the underlying pseudorandom number generator (PRNG) used by random. It may sound like an oxymoron, but this is a way of making random data reproducible and deterministic. That is, if you copy the code here as is, you should get exactly the same histogram because the first call to random.randint() after seeding the generator will produce identical “random” data using the Mersenne Twister.
Building Up From the Base: Histogram Calculations in NumPy
Thus far, you have been working with what could best be called “frequency tables.” But mathematically, a histogram is a mapping of bins (intervals) to frequencies. More technically, it can be used to approximate the probability density function (PDF) of the underlying variable.
Moving on from the “frequency table” above, a true histogram first “bins” the range of values and then counts the number of values that fall into each bin. This is what NumPy’s histogram() function does, and it is the basis for other functions you’ll see here later in Python libraries such as Matplotlib and pandas.
Consider a sample of floats drawn from the Laplace distribution. This distribution has fatter tails than a normal distribution and has two descriptive parameters (location and scale):
>>> import numpy as np
>>> # `numpy.random` uses its own PRNG.
>>> np.random.seed(444)
>>> np.set_printoptions(precision=3)
>>> d = np.random.laplace(loc=15, scale=3, size=500)
>>> d[:5]
array([18.406, 18.087, 16.004, 16.221, 7.358])
In this case, you’re working with a continuous distribution, and it wouldn’t be very helpful to tally each float independently, down to the umpteenth decimal place. Instead, you can bin or “bucket” the data and count the observations that fall into each bin. The histogram is the resulting count of values within each bin:
>>> hist, bin_edges = np.histogram(d)
>>> hist
array([ 1, 0, 3, 4, 4, 10, 13, 9, 2, 4])
>>> bin_edges
array([ 3.217, 5.199, 7.181, 9.163, 11.145, 13.127, 15.109, 17.091,
19.073, 21.055, 23.037])
This result may not be immediately intuitive. np.histogram() by default uses 10 equally sized bins and returns a tuple of the frequency counts and corresponding bin edges. They are edges in the sense that there will be one more bin edge than there are members of the histogram:
>>> hist.size, bin_edges.size
(10, 11)
Technical Detail: All but the last (rightmost) bin is half-open. That is, all bins but the last are [inclusive, exclusive), and the final bin is [inclusive, inclusive].
A very condensed breakdown of how the bins are constructed by NumPy looks like this:
>>> # The leftmost and rightmost bin edges
>>> first_edge, last_edge = a.min(), a.max()
>>> n_equal_bins = 10 # NumPy's default
>>> bin_edges = np.linspace(start=first_edge, stop=last_edge,
... num=n_equal_bins + 1, endpoint=True)
...
>>> bin_edges
array([ 0. , 2.3, 4.6, 6.9, 9.2, 11.5, 13.8, 16.1, 18.4, 20.7, 23. ])
The case above makes a lot of sense: 10 equally spaced bins over a peak-to-peak range of 23 means intervals of width 2.3.
From there, the function delegates to either np.bincount() or np.searchsorted(). bincount() itself can be used to effectively construct the “frequency table” that you started off with here, with the distinction that values with zero occurrences are included:
>>> bcounts = np.bincount(a)
>>> hist, _ = np.histogram(a, range=(0, a.max()), bins=a.max() + 1)
>>> np.array_equal(hist, bcounts)
True
>>> # Reproducing `collections.Counter`
>>> dict(zip(np.unique(a), bcounts[bcounts.nonzero()]))
{0: 1, 1: 3, 2: 1, 3: 1, 7: 2, 23: 1}
Note: hist here is really using bins of width 1.0 rather than “discrete” counts. Hence, this only works for counting integers, not floats such as [3.9, 4.1, 4.15].
Visualizing Histograms with Matplotlib and pandas
Now that you’ve seen how to build a histogram in Python from the ground up, let’s see how other Python packages can do the job for you. Matplotlib provides the functionality to visualize Python histograms out of the box with a versatile wrapper around NumPy’s histogram():
import matplotlib.pyplot as plt
# An "interface" to matplotlib.axes.Axes.hist() method
n, bins, patches = plt.hist(x=d, bins='auto', color='#0504aa',
alpha=0.7, rwidth=0.85)
plt.grid(axis='y', alpha=0.75)
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.title('My Very Own Histogram')
plt.text(23, 45, r'$\mu=15, b=3$')
maxfreq = n.max()
# Set a clean upper y-axis limit.
plt.ylim(ymax=np.ceil(maxfreq / 10) * 10 if maxfreq % 10 else maxfreq + 10)
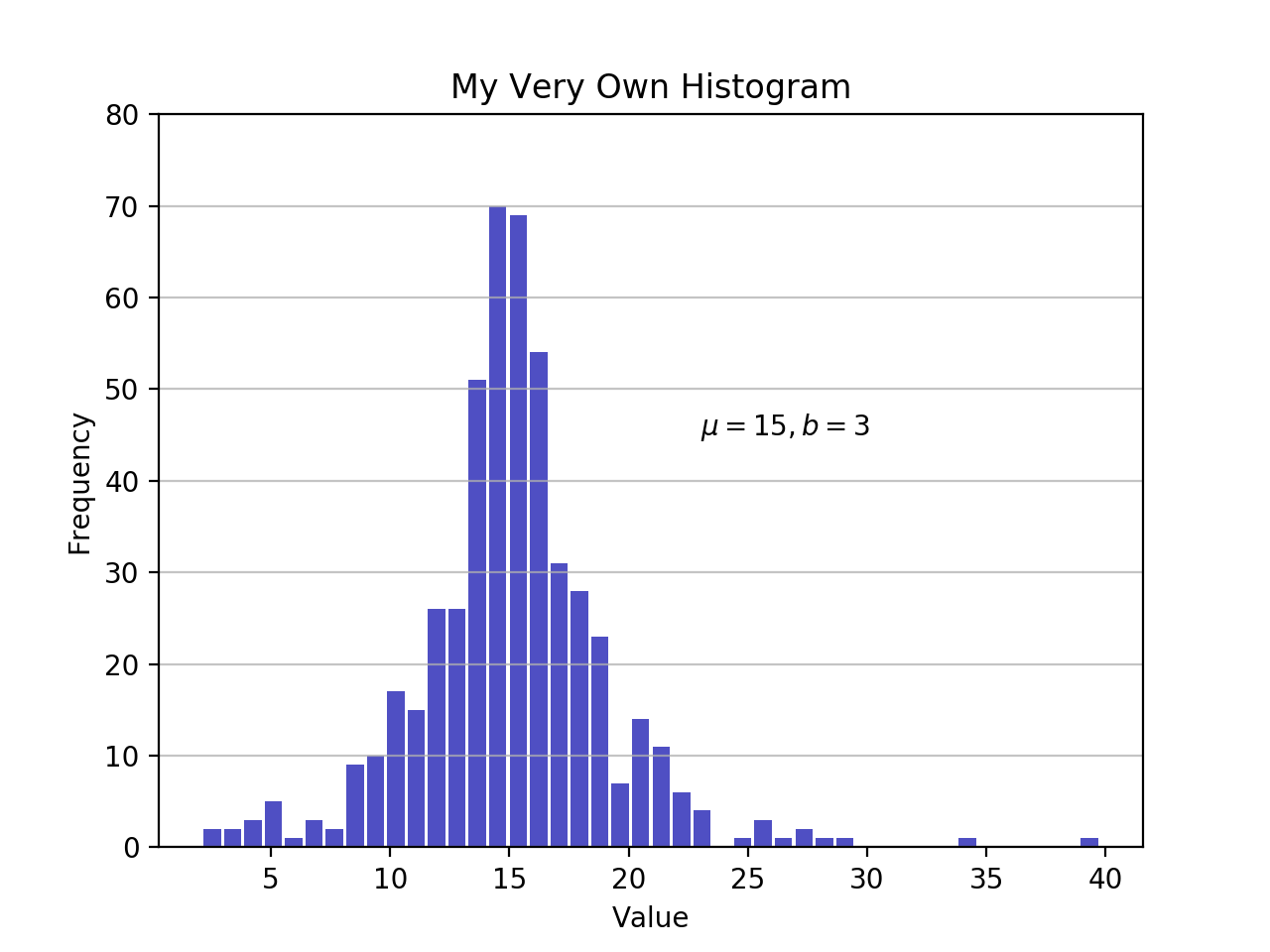
As defined earlier, a plot of a histogram uses its bin edges on the x-axis and the corresponding frequencies on the y-axis. In the chart above, passing bins='auto' chooses between two algorithms to estimate the “ideal” number of bins. At a high level, the goal of the algorithm is to choose a bin width that generates the most faithful representation of the data. For more on this subject, which can get pretty technical, check out Choosing Histogram Bins from the Astropy docs.
Staying in Python’s scientific stack, pandas’ Series.histogram() uses matplotlib.pyplot.hist() to draw a Matplotlib histogram of the input Series:
import pandas as pd
# Generate data on commute times.
size, scale = 1000, 10
commutes = pd.Series(np.random.gamma(scale, size=size) ** 1.5)
commutes.plot.hist(grid=True, bins=20, rwidth=0.9,
color='#607c8e')
plt.title('Commute Times for 1,000 Commuters')
plt.xlabel('Counts')
plt.ylabel('Commute Time')
plt.grid(axis='y', alpha=0.75)

pandas.DataFrame.histogram() is similar but produces a histogram for each column of data in the DataFrame.
Plotting a Kernel Density Estimate (KDE)
In this tutorial, you’ve been working with samples, statistically speaking. Whether the data is discrete or continuous, it’s assumed to be derived from a population that has a true, exact distribution described by just a few parameters.
A kernel density estimation (KDE) is a way to estimate the probability density function (PDF) of the random variable that “underlies” our sample. KDE is a means of data smoothing.
Sticking with the pandas library, you can create and overlay density plots using plot.kde(), which is available for both Series and DataFrame objects. But first, let’s generate two distinct data samples for comparison:
>>> # Sample from two different normal distributions
>>> means = 10, 20
>>> stdevs = 4, 2
>>> dist = pd.DataFrame(
... np.random.normal(loc=means, scale=stdevs, size=(1000, 2)),
... columns=['a', 'b'])
>>> dist.agg(['min', 'max', 'mean', 'std']).round(decimals=2)
a b
min -1.57 12.46
max 25.32 26.44
mean 10.12 19.94
std 3.94 1.94
Now, to plot each histogram on the same Matplotlib axes:
fig, ax = plt.subplots()
dist.plot.kde(ax=ax, legend=False, title='Histogram: A vs. B')
dist.plot.hist(density=True, ax=ax)
ax.set_ylabel('Probability')
ax.grid(axis='y')
ax.set_facecolor('#d8dcd6')

These methods leverage SciPy’s gaussian_kde(), which results in a smoother-looking PDF.
If you take a closer look at this function, you can see how well it approximates the “true” PDF for a relatively small sample of 1000 data points. Below, you can first build the “analytical” distribution with scipy.stats.norm(). This is a class instance that encapsulates the statistical standard normal distribution, its moments, and descriptive functions. Its PDF is “exact” in the sense that it is defined precisely as norm.pdf(x) = exp(-x**2/2) / sqrt(2*pi).
Building from there, you can take a random sample of 1000 datapoints from this distribution, then attempt to back into an estimation of the PDF with scipy.stats.gaussian_kde():
from scipy import stats
# An object representing the "frozen" analytical distribution
# Defaults to the standard normal distribution, N~(0, 1)
dist = stats.norm()
# Draw random samples from the population you built above.
# This is just a sample, so the mean and std. deviation should
# be close to (1, 0).
samp = dist.rvs(size=1000)
# `ppf()`: percent point function (inverse of cdf — percentiles).
x = np.linspace(start=stats.norm.ppf(0.01),
stop=stats.norm.ppf(0.99), num=250)
gkde = stats.gaussian_kde(dataset=samp)
# `gkde.evaluate()` estimates the PDF itself.
fig, ax = plt.subplots()
ax.plot(x, dist.pdf(x), linestyle='solid', c='red', lw=3,
alpha=0.8, label='Analytical (True) PDF')
ax.plot(x, gkde.evaluate(x), linestyle='dashed', c='black', lw=2,
label='PDF Estimated via KDE')
ax.legend(loc='best', frameon=False)
ax.set_title('Analytical vs. Estimated PDF')
ax.set_ylabel('Probability')
ax.text(-2., 0.35, r'$f(x) = \frac{\exp(-x^2/2)}{\sqrt{2*\pi}}$',
fontsize=12)

This is a bigger chunk of code, so let’s take a second to touch on a few key lines:
- SciPy’s
statssubpackage lets you create Python objects that represent analytical distributions that you can sample from to create actual data. Sodist = stats.norm()represents a normal continuous random variable, and you generate random numbers from it withdist.rvs(). - To evaluate both the analytical PDF and the Gaussian KDE, you need an array
xof quantiles (standard deviations above/below the mean, for a normal distribution).stats.gaussian_kde()represents an estimated PDF that you need to evaluate on an array to produce something visually meaningful in this case. - The last line contains some LaTex, which integrates nicely with Matplotlib.
A Fancy Alternative with Seaborn
Let’s bring one more Python package into the mix. Seaborn has a displot() function that plots the histogram and KDE for a univariate distribution in one step. Using the NumPy array d from ealier:
import seaborn as sns
sns.set_style('darkgrid')
sns.distplot(d)

The call above produces a KDE. There is also optionality to fit a specific distribution to the data. This is different than a KDE and consists of parameter estimation for generic data and a specified distribution name:
sns.distplot(d, fit=stats.laplace, kde=False)

Again, note the slight difference. In the first case, you’re estimating some unknown PDF; in the second, you’re taking a known distribution and finding what parameters best describe it given the empirical data.
Other Tools in pandas
In addition to its plotting tools, pandas also offers a convenient .value_counts() method that computes a histogram of non-null values to a pandas Series:
>>> import pandas as pd
>>> data = np.random.choice(np.arange(10), size=10000,
... p=np.linspace(1, 11, 10) / 60)
>>> s = pd.Series(data)
>>> s.value_counts()
9 1831
8 1624
7 1423
6 1323
5 1089
4 888
3 770
2 535
1 347
0 170
dtype: int64
>>> s.value_counts(normalize=True).head()
9 0.1831
8 0.1624
7 0.1423
6 0.1323
5 0.1089
dtype: float64
Elsewhere, pandas.cut() is a convenient way to bin values into arbitrary intervals. Let’s say you have some data on ages of individuals and want to bucket them sensibly:
>>> ages = pd.Series(
... [1, 1, 3, 5, 8, 10, 12, 15, 18, 18, 19, 20, 25, 30, 40, 51, 52])
>>> bins = (0, 10, 13, 18, 21, np.inf) # The edges
>>> labels = ('child', 'preteen', 'teen', 'military_age', 'adult')
>>> groups = pd.cut(ages, bins=bins, labels=labels)
>>> groups.value_counts()
child 6
adult 5
teen 3
military_age 2
preteen 1
dtype: int64
>>> pd.concat((ages, groups), axis=1).rename(columns={0: 'age', 1: 'group'})
age group
0 1 child
1 1 child
2 3 child
3 5 child
4 8 child
5 10 child
6 12 preteen
7 15 teen
8 18 teen
9 18 teen
10 19 military_age
11 20 military_age
12 25 adult
13 30 adult
14 40 adult
15 51 adult
16 52 adult
What’s nice is that both of these operations ultimately utilize Cython code that makes them competitive on speed while maintaining their flexibility.
Alright, So Which Should I Use?
At this point, you’ve seen more than a handful of functions and methods to choose from for plotting a Python histogram. How do they compare? In short, there is no “one-size-fits-all.” Here’s a recap of the functions and methods you’ve covered thus far, all of which relate to breaking down and representing distributions in Python:
| You Have/Want To | Consider Using | Note(s) |
|---|---|---|
| Clean-cut integer data housed in a data structure such as a list, tuple, or set, and you want to create a Python histogram without importing any third party libraries. | collections.Counter() from the Python standard library offers a fast and straightforward way to get frequency counts from a container of data. |
This is a frequency table, so it doesn’t use the concept of binning as a “true” histogram does. |
| Large array of data, and you want to compute the “mathematical” histogram that represents bins and the corresponding frequencies. | NumPy’s np.histogram() and np.bincount() are useful for computing the histogram values numerically and the corresponding bin edges. |
For more, check out np.digitize(). |
Tabular data in pandas’ Series or DataFrame object. |
pandas methods such as Series.plot.hist(), DataFrame.plot.hist(), Series.value_counts(), and cut(), as well as Series.plot.kde() and DataFrame.plot.kde(). |
Check out the pandas visualization docs for inspiration. |
| Create a highly customizable, fine-tuned plot from any data structure. | pyplot.hist() is a widely used histogram plotting function that uses np.histogram() and is the basis for pandas’ plotting functions. |
Matplotlib, and especially its object-oriented framework, is great for fine-tuning the details of a histogram. This interface can take a bit of time to master, but ultimately allows you to be very precise in how any visualization is laid out. |
| Pre-canned design and integration. | Seaborn’s distplot(), for combining a histogram and KDE plot or plotting distribution-fitting. |
Essentially a “wrapper around a wrapper” that leverages a Matplotlib histogram internally, which in turn utilizes NumPy. |
Free Bonus: Short on time? Click here to get access to a free two-page Python histograms cheat sheet that summarizes the techniques explained in this tutorial.
You can also find the code snippets from this article together in one script at the Real Python materials page.
With that, good luck creating histograms in the wild. Hopefully one of the tools above will suit your needs. Whatever you do, just don’t use a pie chart.
Watch Now This tutorial has a related video course created by the Real Python team. Watch it together with the written tutorial to deepen your understanding: Python Histogram Plotting: NumPy, Matplotlib, Pandas & Seaborn





