Correlation coefficients quantify the association between variables or features of a dataset. These statistics are of high importance for science and technology, and Python has great tools that you can use to calculate them. SciPy, NumPy, and pandas correlation methods are fast, comprehensive, and well-documented.
In this tutorial, you’ll learn:
- What Pearson, Spearman, and Kendall correlation coefficients are
- How to use SciPy, NumPy, and pandas correlation functions
- How to visualize data, regression lines, and correlation matrices with Matplotlib
You’ll start with an explanation of correlation, then see three quick introductory examples, and finally dive into details of NumPy, SciPy and pandas correlation.
Free Bonus: Click here to get access to a free NumPy Resources Guide that points you to the best tutorials, videos, and books for improving your NumPy skills.
Correlation
Statistics and data science are often concerned about the relationships between two or more variables (or features) of a dataset. Each data point in the dataset is an observation, and the features are the properties or attributes of those observations.
Every dataset you work with uses variables and observations. For example, you might be interested in understanding the following:
- How the height of basketball players is correlated to their shooting accuracy
- Whether there’s a relationship between employee work experience and salary
- What mathematical dependence exists between the population density and the gross domestic product of different countries
In the examples above, the height, shooting accuracy, years of experience, salary, population density, and gross domestic product are the features or variables. The data related to each player, employee, and each country are the observations.
When data is represented in the form of a table, the rows of that table are usually the observations, while the columns are the features. Take a look at this employee table:
| Name | Years of Experience | Annual Salary |
|---|---|---|
| Ann | 30 | 120,000 |
| Rob | 21 | 105,000 |
| Tom | 19 | 90,000 |
| Ivy | 10 | 82,000 |
In this table, each row represents one observation, or the data about one employee (either Ann, Rob, Tom, or Ivy). Each column shows one property or feature (name, experience, or salary) for all the employees.
If you analyze any two features of a dataset, then you’ll find some type of correlation between those two features. Consider the following figures:
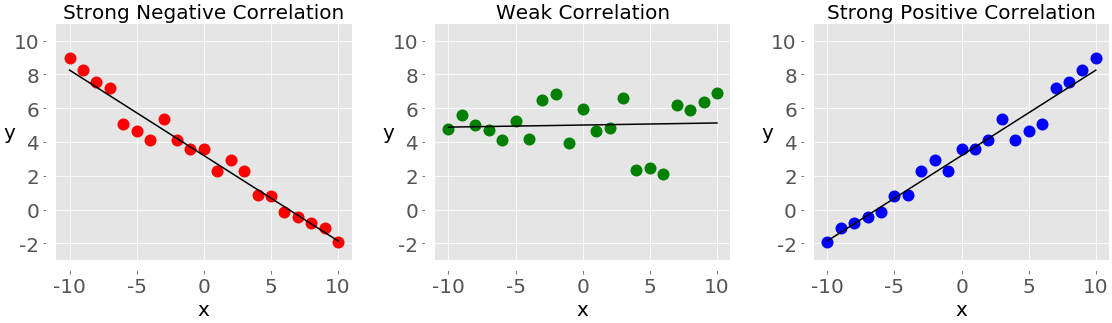
Each of these plots shows one of three different forms of correlation:
-
Negative correlation (red dots): In the plot on the left, the y values tend to decrease as the x values increase. This shows strong negative correlation, which occurs when large values of one feature correspond to small values of the other, and vice versa.
-
Weak or no correlation (green dots): The plot in the middle shows no obvious trend. This is a form of weak correlation, which occurs when an association between two features is not obvious or is hardly observable.
-
Positive correlation (blue dots): In the plot on the right, the y values tend to increase as the x values increase. This illustrates strong positive correlation, which occurs when large values of one feature correspond to large values of the other, and vice versa.
The next figure represents the data from the employee table above:

The correlation between experience and salary is positive because higher experience corresponds to a larger salary and vice versa.
Note: When you’re analyzing correlation, you should always have in mind that correlation does not indicate causation. It quantifies the strength of the relationship between the features of a dataset. Sometimes, the association is caused by a factor common to several features of interest.
Correlation is tightly connected to other statistical quantities like the mean, standard deviation, variance, and covariance. If you want to learn more about these quantities and how to calculate them with Python, then check out Descriptive Statistics with Python.
There are several statistics that you can use to quantify correlation. In this tutorial, you’ll learn about three correlation coefficients:
Pearson’s coefficient measures linear correlation, while the Spearman and Kendall coefficients compare the ranks of data. There are several NumPy, SciPy, and pandas correlation functions and methods that you can use to calculate these coefficients. You can also use Matplotlib to conveniently illustrate the results.
Example: NumPy Correlation Calculation
NumPy has many statistics routines, including np.corrcoef(), that return a matrix of Pearson correlation coefficients. You can start by importing NumPy and defining two NumPy arrays. These are instances of the class ndarray. Call them x and y:
>>> import numpy as np
>>> x = np.arange(10, 20)
>>> x
array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
array([ 2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
Here, you use np.arange() to create an array x of integers between 10 (inclusive) and 20 (exclusive). Then you use np.array() to create a second array y containing arbitrary integers.
Once you have two arrays of the same length, you can call np.corrcoef() with both arrays as arguments:
>>> r = np.corrcoef(x, y)
>>> r
array([[1. , 0.75864029],
[0.75864029, 1. ]])
>>> r[0, 1]
0.7586402890911867
>>> r[1, 0]
0.7586402890911869
corrcoef() returns the correlation matrix, which is a two-dimensional array with the correlation coefficients. Here’s a simplified version of the correlation matrix you just created:
x y
x 1.00 0.76
y 0.76 1.00
The values on the main diagonal of the correlation matrix (upper left and lower right) are equal to 1. The upper left value corresponds to the correlation coefficient for x and x, while the lower right value is the correlation coefficient for y and y. They are always equal to 1.
However, what you usually need are the lower left and upper right values of the correlation matrix. These values are equal and both represent the Pearson correlation coefficient for x and y. In this case, it’s approximately 0.76.
This figure shows the data points and the correlation coefficients for the above example:

The red squares are the data points. As you can see, the figure also shows the values of the three correlation coefficients.
Example: SciPy Correlation Calculation
SciPy also has many statistics routines contained in scipy.stats. You can use the following methods to calculate the three correlation coefficients you saw earlier:
Here’s how you would use these functions in Python:
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> scipy.stats.pearsonr(x, y) # Pearson's r
(0.7586402890911869, 0.010964341301680832)
>>> scipy.stats.spearmanr(x, y) # Spearman's rho
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> scipy.stats.kendalltau(x, y) # Kendall's tau
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)
Note that these functions return objects that contain two values:
- The correlation coefficient
- The p-value
You use the p-value in statistical methods when you’re testing a hypothesis. The p-value is an important measure that requires in-depth knowledge of probability and statistics to interpret. To learn more about them, you can read about the basics or check out a data scientist’s explanation of p-values.
You can extract the p-values and the correlation coefficients with their indices, as the items of tuples:
>>> scipy.stats.pearsonr(x, y)[0] # Pearson's r
0.7586402890911869
>>> scipy.stats.spearmanr(x, y)[0] # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y)[0] # Kendall's tau
0.911111111111111
You could also use dot notation for the Spearman and Kendall coefficients:
>>> scipy.stats.spearmanr(x, y).correlation # Spearman's rho
0.9757575757575757
>>> scipy.stats.kendalltau(x, y).correlation # Kendall's tau
0.911111111111111
The dot notation is longer, but it’s also more readable and more self-explanatory.
If you want to get the Pearson correlation coefficient and p-value at the same time, then you can unpack the return value:
>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829
This approach exploits Python unpacking and the fact that pearsonr() returns a tuple with these two statistics. You can also use this technique with spearmanr() and kendalltau(), as you’ll see later on.
Example: pandas Correlation Calculation
pandas is, in some cases, more convenient than NumPy and SciPy for calculating statistics. It offers statistical methods for Series and DataFrame instances. For example, given two Series objects with the same number of items, you can call .corr() on one of them with the other as the first argument:
>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0 10
1 11
2 12
3 13
4 14
5 15
6 16
7 17
8 18
9 19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0 2
1 1
2 4
3 5
4 8
5 12
6 18
7 25
8 96
9 48
dtype: int64
>>> x.corr(y) # Pearson's r
0.7586402890911867
>>> y.corr(x)
0.7586402890911869
>>> x.corr(y, method='spearman') # Spearman's rho
0.9757575757575757
>>> x.corr(y, method='kendall') # Kendall's tau
0.911111111111111
Here, you use .corr() to calculate all three correlation coefficients. You define the desired statistic with the parameter method, which can take on one of several values:
'pearson''spearman''kendall'- a callable
The callable can be any function, method, or object with .__call__() that accepts two one-dimensional arrays and returns a floating-point number.
Linear Correlation
Linear correlation measures the proximity of the mathematical relationship between variables or dataset features to a linear function. If the relationship between the two features is closer to some linear function, then their linear correlation is stronger and the absolute value of the correlation coefficient is higher.
Pearson Correlation Coefficient
Consider a dataset with two features: x and y. Each feature has n values, so x and y are n-tuples. Say that the first value x₁ from x corresponds to the first value y₁ from y, the second value x₂ from x to the second value y₂ from y, and so on. Then, there are n pairs of corresponding values: (x₁, y₁), (x₂, y₂), and so on. Each of these x-y pairs represents a single observation.
The Pearson (product-moment) correlation coefficient is a measure of the linear relationship between two features. It’s the ratio of the covariance of x and y to the product of their standard deviations. It’s often denoted with the letter r and called Pearson’s r. You can express this value mathematically with this equation:
r = Σᵢ((xᵢ − mean(x))(yᵢ − mean(y))) (√Σᵢ(xᵢ − mean(x))² √Σᵢ(yᵢ − mean(y))²)⁻¹
Here, i takes on the values 1, 2, …, n. The mean values of x and y are denoted with mean(x) and mean(y). This formula shows that if larger x values tend to correspond to larger y values and vice versa, then r is positive. On the other hand, if larger x values are mostly associated with smaller y values and vice versa, then r is negative.
Here are some important facts about the Pearson correlation coefficient:
-
The Pearson correlation coefficient can take on any real value in the range −1 ≤ r ≤ 1.
-
The maximum value r = 1 corresponds to the case in which there’s a perfect positive linear relationship between x and y. In other words, larger x values correspond to larger y values and vice versa.
-
The value r > 0 indicates positive correlation between x and y.
-
The value r = 0 corresponds to the case in which there’s no linear relationship between x and y.
-
The value r < 0 indicates negative correlation between x and y.
-
The minimal value r = −1 corresponds to the case when there’s a perfect negative linear relationship between x and y. In other words, larger x values correspond to smaller y values and vice versa.
The above facts can be summed up in the following table:
| Pearson’s r Value | Correlation Between x and y |
|---|---|
| equal to 1 | perfect positive linear relationship |
| greater than 0 | positive correlation |
| equal to 0 | no linear relationship |
| less than 0 | negative correlation |
| equal to -1 | perfect negative linear relationship |
In short, a larger absolute value of r indicates stronger correlation, closer to a linear function. A smaller absolute value of r indicates weaker correlation.
Linear Regression: SciPy Implementation
Linear regression is the process of finding the linear function that is as close as possible to the actual relationship between features. In other words, you determine the linear function that best describes the association between the features. This linear function is also called the regression line.
You can implement linear regression with SciPy. You’ll get the linear function that best approximates the relationship between two arrays, as well as the Pearson correlation coefficient. To get started, you first need to import the libraries and prepare some data to work with:
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
Here, you import numpy and scipy.stats and define the variables x and y.
You can use scipy.stats.linregress() to perform linear regression for two arrays of the same length. You should provide the arrays as the arguments and get the outputs by using dot notation:
>>> result = scipy.stats.linregress(x, y)
>>> result.slope
7.4363636363636365
>>> result.intercept
-85.92727272727274
>>> result.rvalue
0.7586402890911869
>>> result.pvalue
0.010964341301680825
>>> result.stderr
2.257878767543913
That’s it! You’ve completed the linear regression and gotten the following results:
.slope: the slope of the regression line.intercept: the intercept of the regression line.pvalue: the p-value.stderr: the standard error of the estimated gradient
You’ll learn how to visualize these results in a later section.
You can also provide a single argument to linregress(), but it must be a two-dimensional array with one dimension of length two:
>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> scipy.stats.linregress(xy)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)
The result is exactly the same as the previous example because xy contains the same data as x and y together. linregress() took the first row of xy as one feature and the second row as the other feature.
Note: In the example above, scipy.stats.linregress() considers the rows as features and columns as observations. That’s because there are two rows.
The usual practice in machine learning is the opposite: rows are observations and columns are features. Many machine learning libraries, like pandas, Scikit-Learn, Keras, and others, follow this convention.
You should be careful to note how the observations and features are indicated whenever you’re analyzing correlation in a dataset.
linregress() will return the same result if you provide the transpose of xy, or a NumPy array with 10 rows and two columns. In NumPy, you can transpose a matrix in many ways:
Here’s how you might transpose xy:
>>> xy.T
array([[10, 2],
[11, 1],
[12, 4],
[13, 5],
[14, 8],
[15, 12],
[16, 18],
[17, 25],
[18, 96],
[19, 48]])
Now that you know how to get the transpose, you can pass one to linregress(). The first column will be one feature and the second column the other feature:
>>> scipy.stats.linregress(xy.T)
LinregressResult(slope=7.4363636363636365, intercept=-85.92727272727274, rvalue=0.7586402890911869, pvalue=0.010964341301680825, stderr=2.257878767543913)
Here, you use .T to get the transpose of xy. linregress() works the same way with xy and its transpose. It extracts the features by splitting the array along the dimension with length two.
You should also be careful to note whether or not your dataset contains missing values. In data science and machine learning, you’ll often find some missing or corrupted data. The usual way to represent it in Python, NumPy, SciPy, and pandas is by using NaN or Not a Number values. But if your data contains nan values, then you won’t get a useful result with linregress():
>>> scipy.stats.linregress(np.arange(3), np.array([2, np.nan, 5]))
LinregressResult(slope=nan, intercept=nan, rvalue=nan, pvalue=nan, stderr=nan)
In this case, your resulting object returns all nan values. In Python, nan is a special floating-point value that you can get by using any of the following:
You can also check whether a variable corresponds to nan with math.isnan() or numpy.isnan().
Pearson Correlation: NumPy and SciPy Implementation
You’ve already seen how to get the Pearson correlation coefficient with corrcoef() and pearsonr():
>>> r, p = scipy.stats.pearsonr(x, y)
>>> r
0.7586402890911869
>>> p
0.010964341301680829
>>> np.corrcoef(x, y)
array([[1. , 0.75864029],
[0.75864029, 1. ]])
Note that if you provide an array with a nan value to pearsonr(), you’ll get a ValueError.
There are few additional details worth considering. First, recall that np.corrcoef() can take two NumPy arrays as arguments. Instead, you can pass a single two-dimensional array with the same values as the argument:
>>> np.corrcoef(xy)
array([[1. , 0.75864029],
[0.75864029, 1. ]])
The results are the same in this and previous examples. Again, the first row of xy represents one feature, while the second row represents the other.
If you want to get the correlation coefficients for three features, then you just provide a numeric two-dimensional array with three rows as the argument:
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> np.corrcoef(xyz)
array([[ 1. , 0.75864029, -0.96807242],
[ 0.75864029, 1. , -0.83407922],
[-0.96807242, -0.83407922, 1. ]])
You’ll obtain the correlation matrix again, but this one will be larger than previous ones:
x y z
x 1.00 0.76 -0.97
y 0.76 1.00 -0.83
z -0.97 -0.83 1.00
This is because corrcoef() considers each row of xyz as one feature. The value 0.76 is the correlation coefficient for the first two features of xyz. This is the same as the coefficient for x and y in previous examples. -0.97 represents Pearson’s r for the first and third features, while -0.83 is Pearson’s r for the last two features.
Here’s an interesting example of what happens when you pass nan data to corrcoef():
>>> arr_with_nan = np.array([[0, 1, 2, 3],
... [2, 4, 1, 8],
... [2, 5, np.nan, 2]])
>>> np.corrcoef(arr_with_nan)
array([[1. , 0.62554324, nan],
[0.62554324, 1. , nan],
[ nan, nan, nan]])
In this example, the first two rows (or features) of arr_with_nan are okay, but the third row [2, 5, np.nan, 2] contains a nan value. Everything that doesn’t include the feature with nan is calculated well. The results that depend on the last row, however, are nan.
By default, numpy.corrcoef() considers the rows as features and the columns as observations. If you want the opposite behavior, which is widely used in machine learning, then use the argument rowvar=False:
>>> xyz.T
array([[ 10, 2, 5],
[ 11, 1, 3],
[ 12, 4, 2],
[ 13, 5, 1],
[ 14, 8, 0],
[ 15, 12, -2],
[ 16, 18, -8],
[ 17, 25, -11],
[ 18, 96, -15],
[ 19, 48, -16]])
>>> np.corrcoef(xyz.T, rowvar=False)
array([[ 1. , 0.75864029, -0.96807242],
[ 0.75864029, 1. , -0.83407922],
[-0.96807242, -0.83407922, 1. ]])
This array is identical to the one you saw earlier. Here, you apply a different convention, but the result is the same.
Pearson Correlation: pandas Implementation
So far, you’ve used Series and DataFrame object methods to calculate correlation coefficients. Let’s explore these methods in more detail. First, you need to import pandas and create some instances of Series and DataFrame:
>>> import pandas as pd
>>> x = pd.Series(range(10, 20))
>>> x
0 10
1 11
2 12
3 13
4 14
5 15
6 16
7 17
8 18
9 19
dtype: int64
>>> y = pd.Series([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> y
0 2
1 1
2 4
3 5
4 8
5 12
6 18
7 25
8 96
9 48
dtype: int64
>>> z = pd.Series([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> z
0 5
1 3
2 2
3 1
4 0
5 -2
6 -8
7 -11
8 -15
9 -16
dtype: int64
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xy
x-values y-values
0 10 2
1 11 1
2 12 4
3 13 5
4 14 8
5 15 12
6 16 18
7 17 25
8 18 96
9 19 48
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})
>>> xyz
x-values y-values z-values
0 10 2 5
1 11 1 3
2 12 4 2
3 13 5 1
4 14 8 0
5 15 12 -2
6 16 18 -8
7 17 25 -11
8 18 96 -15
9 19 48 -16
You now have three Series objects called x, y, and z. You also have two DataFrame objects, xy and xyz.
Note: When you work with DataFrame instances, you should be aware that the rows are observations and the columns are features. This is consistent with the usual practice in machine learning.
You’ve already learned how to use .corr() with Series objects to get the Pearson correlation coefficient:
>>> x.corr(y)
0.7586402890911867
Here, you call .corr() on one object and pass the other as the first argument.
If you provide a nan value, then .corr() will still work, but it will exclude observations that contain nan values:
>>> u, u_with_nan = pd.Series([1, 2, 3]), pd.Series([1, 2, np.nan, 3])
>>> v, w = pd.Series([1, 4, 8]), pd.Series([1, 4, 154, 8])
>>> u.corr(v)
0.9966158955401239
>>> u_with_nan.corr(w)
0.9966158955401239
You get the same value of the correlation coefficient in these two examples. That’s because .corr() ignores the pair of values (np.nan, 154) that has a missing value.
You can also use .corr() with DataFrame objects. You can use it to get the correlation matrix for their columns:
>>> corr_matrix = xy.corr()
>>> corr_matrix
x-values y-values
x-values 1.00000 0.75864
y-values 0.75864 1.00000
The resulting correlation matrix is a new instance of DataFrame and holds the correlation coefficients for the columns xy['x-values'] and xy['y-values']. Such labeled results are usually very convenient to work with because you can access them with either their labels or their integer position indices:
>>> corr_matrix.at['x-values', 'y-values']
0.7586402890911869
>>> corr_matrix.iat[0, 1]
0.7586402890911869
This example shows two ways of accessing values:
- Use
.at[]to access a single value by row and column labels. - Use
.iat[]to access a value by the positions of its row and column.
You can apply .corr() the same way with DataFrame objects that contain three or more columns:
>>> xyz.corr()
x-values y-values z-values
x-values 1.000000 0.758640 -0.968072
y-values 0.758640 1.000000 -0.834079
z-values -0.968072 -0.834079 1.000000
You’ll get a correlation matrix with the following correlation coefficients:
0.758640forx-valuesandy-values-0.968072forx-valuesandz-values-0.834079fory-valuesandz-values
Another useful method is .corrwith(), which allows you to calculate the correlation coefficients between the rows or columns of one DataFrame object and another Series or DataFrame object passed as the first argument:
>>> xy.corrwith(z)
x-values -0.968072
y-values -0.834079
dtype: float64
In this case, the result is a new Series object with the correlation coefficient for the column xy['x-values'] and the values of z, as well as the coefficient for xy['y-values'] and z.
.corrwith() has the optional parameter axis that specifies whether columns or rows represent the features. The default value of axis is 0, and it also defaults to columns representing features. There’s also a drop parameter, which indicates what to do with missing values.
Both .corr() and .corrwith() have the optional parameter method to specify the correlation coefficient that you want to calculate. The Pearson correlation coefficient is returned by default, so you don’t need to provide it in this case.
Rank Correlation
Rank correlation compares the ranks or the orderings of the data related to two variables or dataset features. If the orderings are similar, then the correlation is strong, positive, and high. However, if the orderings are close to reversed, then the correlation is strong, negative, and low. In other words, rank correlation is concerned only with the order of values, not with the particular values from the dataset.
To illustrate the difference between linear and rank correlation, consider the following figure:

The left plot has a perfect positive linear relationship between x and y, so r = 1. The central plot shows positive correlation and the right one shows negative correlation. However, neither of them is a linear function, so r is different than −1 or 1.
When you look only at the orderings or ranks, all three relationships are perfect! The left and central plots show the observations where larger x values always correspond to larger y values. This is perfect positive rank correlation. The right plot illustrates the opposite case, which is perfect negative rank correlation.
Spearman Correlation Coefficient
The Spearman correlation coefficient between two features is the Pearson correlation coefficient between their rank values. It’s calculated the same way as the Pearson correlation coefficient but takes into account their ranks instead of their values. It’s often denoted with the Greek letter rho (ρ) and called Spearman’s rho.
Say you have two n-tuples, x and y, where (x₁, y₁), (x₂, y₂), … are the observations as pairs of corresponding values. You can calculate the Spearman correlation coefficient ρ the same way as the Pearson coefficient. You’ll use the ranks instead of the actual values from x and y.
Here are some important facts about the Spearman correlation coefficient:
-
It can take a real value in the range −1 ≤ ρ ≤ 1.
-
Its maximum value ρ = 1 corresponds to the case when there’s a monotonically increasing function between x and y. In other words, larger x values correspond to larger y values and vice versa.
-
Its minimum value ρ = −1 corresponds to the case when there’s a monotonically decreasing function between x and y. In other words, larger x values correspond to smaller y values and vice versa.
You can calculate Spearman’s rho in Python in a very similar way as you would Pearson’s r.
Kendall Correlation Coefficient
Let’s start again by considering two n-tuples, x and y. Each of the x-y pairs (x₁, y₁), (x₂, y₂), … is a single observation. A pair of observations (xᵢ, yᵢ) and (xⱼ, yⱼ), where i < j, will be one of three things:
- concordant if either (xᵢ > xⱼ and yᵢ > yⱼ) or (xᵢ < xⱼ and yᵢ < yⱼ)
- discordant if either (xᵢ < xⱼ and yᵢ > yⱼ) or (xᵢ > xⱼ and yᵢ < yⱼ)
- neither if there’s a tie in x (xᵢ = xⱼ) or a tie in y (yᵢ = yⱼ)
The Kendall correlation coefficient compares the number of concordant and discordant pairs of data. This coefficient is based on the difference in the counts of concordant and discordant pairs relative to the number of x-y pairs. It’s often denoted with the Greek letter tau (τ) and called Kendall’s tau.
According to the scipy.stats official docs, the Kendall correlation coefficient is calculated as
τ = (n⁺ − n⁻) / √((n⁺ + n⁻ + nˣ)(n⁺ + n⁻ + nʸ)),
where:
- n⁺ is the number of concordant pairs
- n⁻ is the number of discordant pairs
- nˣ is the number of ties only in x
- nʸ is the number of ties only in y
If a tie occurs in both x and y, then it’s not included in either nˣ or nʸ.
The Wikipedia page on Kendall rank correlation coefficient gives the following expression: τ = (2 / (n(n − 1))) Σᵢⱼ(sign(xᵢ − xⱼ) sign(yᵢ − yⱼ)) for i < j, where i = 1, 2, …, n − 1 and j = 2, 3, …, n. The sign function sign(z) is −1 if z < 0, 0 if z = 0, and 1 if z > 0. n(n − 1) / 2 is the total number of x-y pairs.
Some important facts about the Kendall correlation coefficient are as follows:
-
It can take a real value in the range −1 ≤ τ ≤ 1.
-
Its maximum value τ = 1 corresponds to the case when the ranks of the corresponding values in x and y are the same. In other words, all pairs are concordant.
-
Its minimum value τ = −1 corresponds to the case when the rankings in x are the reverse of the rankings in y. In other words, all pairs are discordant.
You can calculate Kendall’s tau in Python similarly to how you would calculate Pearson’s r.
Rank: SciPy Implementation
You can use scipy.stats to determine the rank for each value in an array. First, you’ll import the libraries and create NumPy arrays:
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
Now that you’ve prepared data, you can determine the rank of each value in a NumPy array with scipy.stats.rankdata():
>>> scipy.stats.rankdata(x)
array([ 1., 2., 3., 4., 5., 6., 7., 8., 9., 10.])
>>> scipy.stats.rankdata(y)
array([ 2., 1., 3., 4., 5., 6., 7., 8., 10., 9.])
>>> scipy.stats.rankdata(z)
array([10., 9., 8., 7., 6., 5., 4., 3., 2., 1.])
The arrays x and z are monotonic, so their ranks are monotonic as well. The smallest value in y is 1 and it corresponds to the rank 1. The second smallest is 2, which corresponds to the rank 2. The largest value is 96, which corresponds to the largest rank 10 since there are 10 items in the array.
rankdata() has the optional parameter method. This tells Python what to do if there are ties in the array (if two or more values are equal). By default, it assigns them the average of the ranks:
>>> scipy.stats.rankdata([8, 2, 0, 2])
array([4. , 2.5, 1. , 2.5])
There are two elements with a value of 2 and they have the ranks 2.0 and 3.0. The value 0 has rank 1.0 and the value 8 has rank 4.0. Then, both elements with the value 2 will get the same rank 2.5.
rankdata() treats nan values as if they were large:
>>> scipy.stats.rankdata([8, np.nan, 0, 2])
array([3., 4., 1., 2.])
In this case, the value np.nan corresponds to the largest rank 4.0. You can also get ranks with np.argsort():
>>> np.argsort(y) + 1
array([ 2, 1, 3, 4, 5, 6, 7, 8, 10, 9])
argsort() returns the indices that the array items would have in the sorted array. These indices are zero-based, so you’ll need to add 1 to all of them.
Rank Correlation: NumPy and SciPy Implementation
You can calculate the Spearman correlation coefficient with scipy.stats.spearmanr():
>>> result = scipy.stats.spearmanr(x, y)
>>> result
SpearmanrResult(correlation=0.9757575757575757, pvalue=1.4675461874042197e-06)
>>> result.correlation
0.9757575757575757
>>> result.pvalue
1.4675461874042197e-06
>>> rho, p = scipy.stats.spearmanr(x, y)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06
spearmanr() returns an object that contains the value of the Spearman correlation coefficient and p-value. As you can see, you can access particular values in two ways:
- Using dot notation (
result.correlationandresult.pvalue) - Using Python unpacking (
rho, p = scipy.stats.spearmanr(x, y))
You can get the same result if you provide the two-dimensional array xy that contains the same data as x and y to spearmanr():
>>> xy = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48]])
>>> rho, p = scipy.stats.spearmanr(xy, axis=1)
>>> rho
0.9757575757575757
>>> p
1.4675461874042197e-06
The first row of xy is one feature, while the second row is the other feature. You can modify this. The optional parameter axis determines whether columns (axis=0) or rows (axis=1) represent the features. The default behavior is that the rows are observations and the columns are features.
Another optional parameter nan_policy defines how to handle nan values. It can take one of three values:
'propagate'returnsnanif there’s ananvalue among the inputs. This is the default behavior.'raise'raises aValueErrorif there’s ananvalue among the inputs.'omit'ignores the observations withnanvalues.
If you provide a two-dimensional array with more than two features, then you’ll get the correlation matrix and the matrix of the p-values:
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
>>> corr_matrix, p_matrix = scipy.stats.spearmanr(xyz, axis=1)
>>> corr_matrix
array([[ 1. , 0.97575758, -1. ],
[ 0.97575758, 1. , -0.97575758],
[-1. , -0.97575758, 1. ]])
>>> p_matrix
array([[6.64689742e-64, 1.46754619e-06, 6.64689742e-64],
[1.46754619e-06, 6.64689742e-64, 1.46754619e-06],
[6.64689742e-64, 1.46754619e-06, 6.64689742e-64]])
The value -1 in the correlation matrix shows that the first and third features have a perfect negative rank correlation, that is that larger values in the first row always correspond to smaller values in the third.
You can obtain the Kendall correlation coefficient with kendalltau():
>>> result = scipy.stats.kendalltau(x, y)
>>> result
KendalltauResult(correlation=0.911111111111111, pvalue=2.9761904761904762e-05)
>>> result.correlation
0.911111111111111
>>> result.pvalue
2.9761904761904762e-05
>>> tau, p = scipy.stats.kendalltau(x, y)
>>> tau
0.911111111111111
>>> p
2.9761904761904762e-05
kendalltau() works much like spearmanr(). It takes two one-dimensional arrays, has the optional parameter nan_policy, and returns an object with the values of the correlation coefficient and p-value.
However, if you provide only one two-dimensional array as an argument, then kendalltau() will raise a TypeError. If you pass two multi-dimensional arrays of the same shape, then they’ll be flattened before the calculation.
Rank Correlation: pandas Implementation
You can calculate the Spearman and Kendall correlation coefficients with pandas. Just like before, you start by importing pandas and creating some Series and DataFrame instances:
>>> import pandas as pd
>>> x, y, z = pd.Series(x), pd.Series(y), pd.Series(z)
>>> xy = pd.DataFrame({'x-values': x, 'y-values': y})
>>> xyz = pd.DataFrame({'x-values': x, 'y-values': y, 'z-values': z})
Now that you have these pandas objects, you can use .corr() and .corrwith() just like you did when you calculated the Pearson correlation coefficient. You just need to specify the desired correlation coefficient with the optional parameter method, which defaults to 'pearson'.
To calculate Spearman’s rho, pass method=spearman:
>>> x.corr(y, method='spearman')
0.9757575757575757
>>> xy.corr(method='spearman')
x-values y-values
x-values 1.000000 0.975758
y-values 0.975758 1.000000
>>> xyz.corr(method='spearman')
x-values y-values z-values
x-values 1.000000 0.975758 -1.000000
y-values 0.975758 1.000000 -0.975758
z-values -1.000000 -0.975758 1.000000
>>> xy.corrwith(z, method='spearman')
x-values -1.000000
y-values -0.975758
dtype: float64
If you want Kendall’s tau, then you use method=kendall:
>>> x.corr(y, method='kendall')
0.911111111111111
>>> xy.corr(method='kendall')
x-values y-values
x-values 1.000000 0.911111
y-values 0.911111 1.000000
>>> xyz.corr(method='kendall')
x-values y-values z-values
x-values 1.000000 0.911111 -1.000000
y-values 0.911111 1.000000 -0.911111
z-values -1.000000 -0.911111 1.000000
>>> xy.corrwith(z, method='kendall')
x-values -1.000000
y-values -0.911111
dtype: float64
As you can see, unlike with SciPy, you can use a single two-dimensional data structure (a dataframe).
Visualization of Correlation
Data visualization is very important in statistics and data science. It can help you better understand your data and give you a better insight into the relationships between features. In this section, you’ll learn how to visually represent the relationship between two features with an x-y plot. You’ll also use heatmaps to visualize a correlation matrix.
You’ll learn how to prepare data and get certain visual representations, but you won’t cover many other explanations. To learn more about Matplotlib in-depth, check out Python Plotting With Matplotlib (Guide). You can also take a look at the official documentation and Anatomy of Matplotlib.
To get started, first import matplotlib.pyplot:
>>> import matplotlib.pyplot as plt
>>> plt.style.use('ggplot')
Here, you use plt.style.use('ggplot') to set the style of the plots. Feel free to skip this line if you want.
You’ll use the arrays x, y, z, and xyz from the previous sections. You can create them again to cut down on scrolling:
>>> import numpy as np
>>> import scipy.stats
>>> x = np.arange(10, 20)
>>> y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 96, 48])
>>> z = np.array([5, 3, 2, 1, 0, -2, -8, -11, -15, -16])
>>> xyz = np.array([[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
... [2, 1, 4, 5, 8, 12, 18, 25, 96, 48],
... [5, 3, 2, 1, 0, -2, -8, -11, -15, -16]])
Now that you’ve got your data, you’re ready to plot.
X-Y Plots With a Regression Line
First, you’ll see how to create an x-y plot with the regression line, its equation, and the Pearson correlation coefficient. You can get the slope and the intercept of the regression line, as well as the correlation coefficient, with linregress():
>>> slope, intercept, r, p, stderr = scipy.stats.linregress(x, y)
Now you have all the values you need. You can also get the string with the equation of the regression line and the value of the correlation coefficient. f-strings are very convenient for this purpose:
>>> line = f'Regression line: y={intercept:.2f}+{slope:.2f}x, r={r:.2f}'
>>> line
'Regression line: y=-85.93+7.44x, r=0.76'
Now, create the x-y plot with .plot():
fig, ax = plt.subplots()
ax.plot(x, y, linewidth=0, marker='s', label='Data points')
ax.plot(x, intercept + slope * x, label=line)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend(facecolor='white')
plt.show()
Your output should look like this:

The red squares represent the observations, while the blue line is the regression line. Its equation is listed in the legend, together with the correlation coefficient.
Heatmaps of Correlation Matrices
The correlation matrix can become really big and confusing when you have a lot of features! Fortunately, you can present it visually as a heatmap where each field has the color that corresponds to its value. You’ll need the correlation matrix:
>>> corr_matrix = np.corrcoef(xyz).round(decimals=2)
>>> corr_matrix
array([[ 1. , 0.76, -0.97],
[ 0.76, 1. , -0.83],
[-0.97, -0.83, 1. ]])
It can be convenient for you to round the numbers in the correlation matrix with .round(), as they’re going to be shown be on the heatmap.
Finally, create your heatmap with .imshow() and the correlation matrix as its argument:
fig, ax = plt.subplots()
im = ax.imshow(corr_matrix)
im.set_clim(-1, 1)
ax.grid(False)
ax.xaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.yaxis.set(ticks=(0, 1, 2), ticklabels=('x', 'y', 'z'))
ax.set_ylim(2.5, -0.5)
for i in range(3):
for j in range(3):
ax.text(j, i, corr_matrix[i, j], ha='center', va='center',
color='r')
cbar = ax.figure.colorbar(im, ax=ax, format='% .2f')
plt.show()
Your output should look like this:
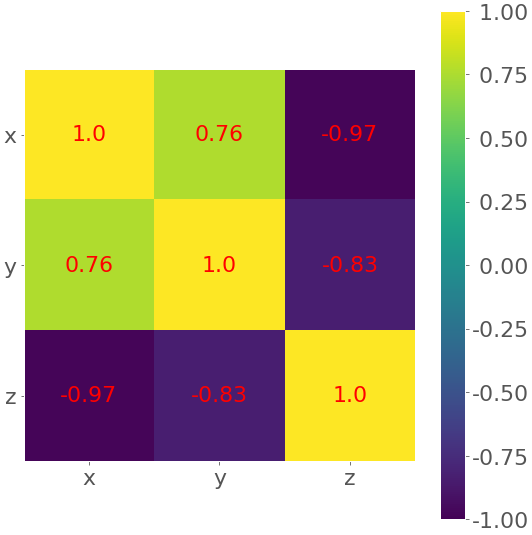
The result is a table with the coefficients. It sort of looks like the pandas output with colored backgrounds. The colors help you interpret the output. In this example, the yellow color represents the number 1, green corresponds to 0.76, and purple is used for the negative numbers.
Conclusion
You now know that correlation coefficients are statistics that measure the association between variables or features of datasets. They’re very important in data science and machine learning.
You can now use Python to calculate:
- Pearson’s product-moment correlation coefficient
- Spearman’s rank correlation coefficient
- Kendall’s rank correlation coefficient
Now you can use NumPy, SciPy, and pandas correlation functions and methods to effectively calculate these (and other) statistics, even when you work with large datasets. You also know how to visualize data, regression lines, and correlation matrices with Matplotlib plots and heatmaps.
If you have any questions or comments, please put them in the comments section below!







